Let f(x) ={−X2+(b3−b2+b−1)(b2+3b+2)}2X−3 1<X<30≤X<1
Find al possible values of b such that f(x) has the smallest values at x=1
Video Solution
Text Solution
Such problems can easily be solved by graphical approach (as in figure).
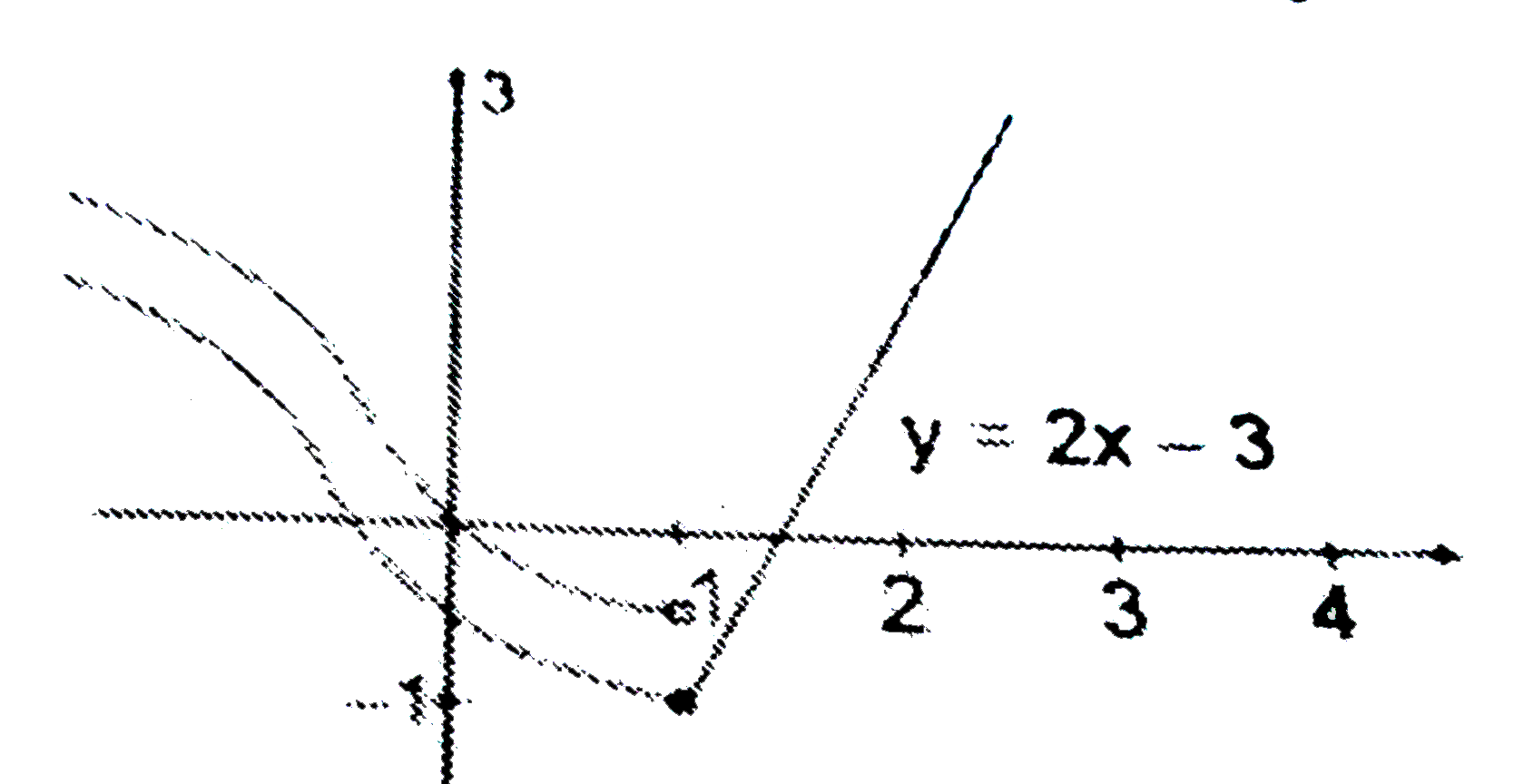
Hence the limiting value of f(x) from of x=1 should b either greater of equal to the value of function at x=1.
limx→1f(x)≤f(1)
⇒ −1+(b3−b2+b−1)(b2+3b+2)≤−1
⇒ (b2+1)(b−1)(b+1)(b+2)≥0
⇒ b∈(−2,−1)∪[1,+∞)
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems
34 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A
5 Videos
- COMBINATORICSBOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
8 Videos
Similar Questions
Knowledge Check
Let f(x)={3x2−2x+10x<1−2x>1
The set of values of b for which f(x) has greatest value at x=1 isA(−6,−2)B(2,6)C(−6,−2)∪(2,6)D(−6,6)The function f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x2/a0≤x<1a1≤x<√2(2b2−4b)/x2√2≤x<∞ is continuous for 0≤x<∞, then the most suitable values of a and b are
Aa=1, b=-1Ba=−1,b=1+√2Ca=−1,b=1Dnone of theseIf f(x) =x2a, if 0≤x<1=a, if 1≤x<√2=2b2−4bx2, if √2≤x
is continuous in (0,∞) , then the most suitable values of a and b ( in that order ) areA1,−1B−1,1+√2C−1,1D−1,−1
Let f(x)=⎧⎪⎨⎪⎩x,x<12−x∣,1<x≤2thenf(x)is−2+3x−x2,x>2
View SolutionLet f(x)={a−3x−2≤x<04x±30≤x<1,iff(x) has smallest valueat x=0, then range of a, is
View SolutionIf f(x) =−x2, if x≤0=5x−4, if 0<x≤1=4x2−3x, if 1<x≤2 then f is
View SolutionIf f(x)=⎧⎪⎨⎪⎩ax2−b, for 0≤x<12, for x=1x+1, for 1<x≤2 is continuous at x=1 , then the most suitable values of a, b are
View SolutionIf f(x) =ax2+b, if 0≤x<1=x+3, if 1<x≤2=4, if x=1
then the values of (a,b) for which f(x) cannot be continuous at x = 1 are
View Solution
