The area cut off from a parabola by any double ordinate is k time the corresponding rectangle contained by the double ordinate and its distance from the vertex. Find the value of k ?
Video Solution
Text Solution
Consider y2=4ax,a>0 and x=c
Area by double ordinate =2c∫02√a√xdx=83√ac3/2
Area by double ordinate = k (Area of rectangle)
83√ac3/2=k4√ac3/2⇒k=23
(b) If f(x)<0 for x∈[a,b] then area bounded by curve y=f(x), axis x=a and x=b is - b∫xf(x)dx
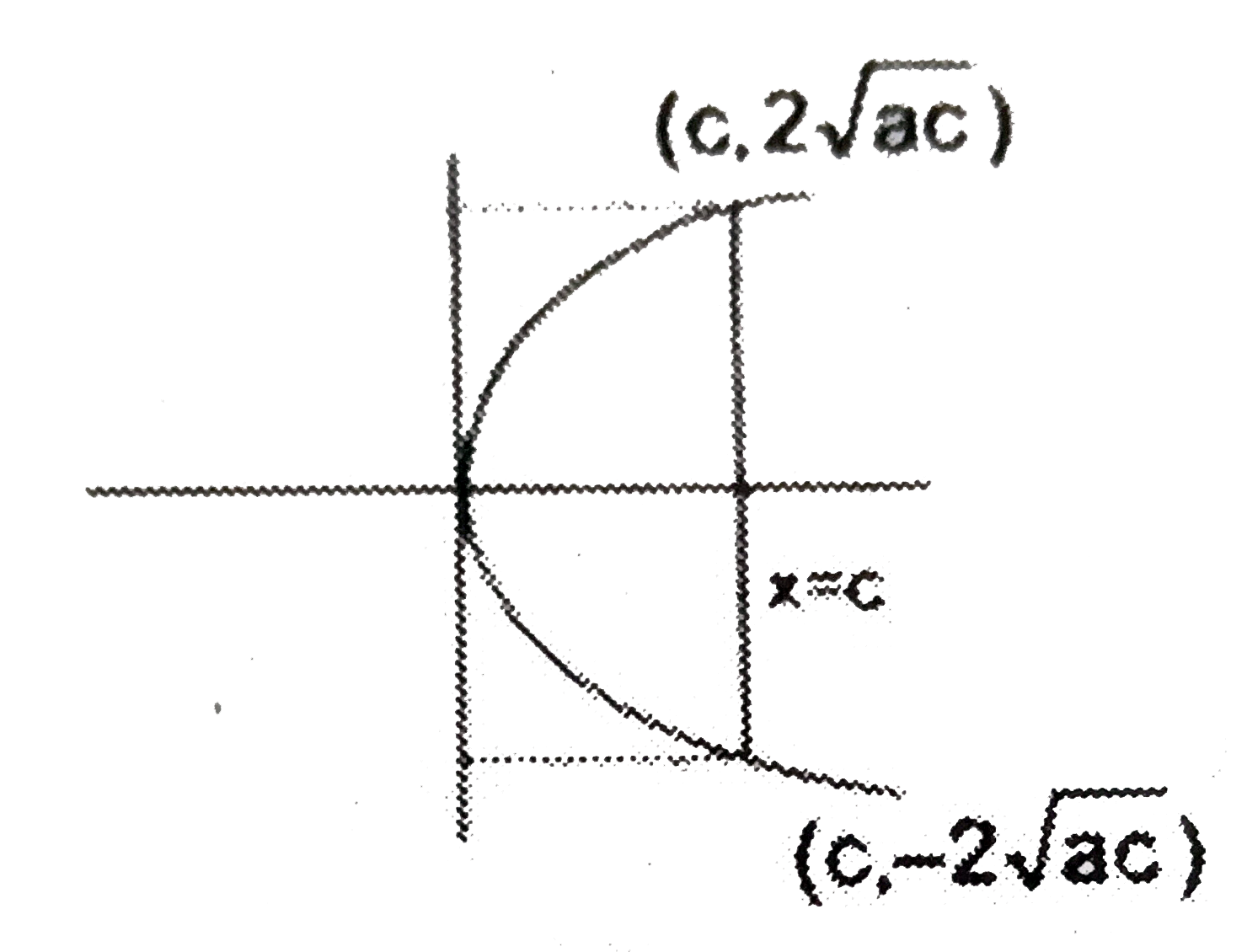

|
Topper's Solved these Questions
- DEFINITE INTEGRATION & ITS APPLICATION Book:RESONANCEChapter:DEFINITE INTEGRATION & ITS APPLICATION Exercise:Self practive problem
Explore 56 Videos
- DEFINITE INTEGRATION & ITS APPLICATION Book:RESONANCEChapter:DEFINITE INTEGRATION & ITS APPLICATION Exercise:Exercise 1
Explore 31 Videos
- COMBINATORICSBook:RESONANCEChapter:COMBINATORICSExercise:Exercise-2 (Part-II: Previously Asked Question of RMO)
Explore 8 Videos
- DPPBook:RESONANCEChapter:DPPExercise:QUESTION
Explore 665 Videos
Similar Questions
Knowledge Check
The area cut off from a parabola by any double ordinate is k time the corresponding rectangle contained by the double ordinate and its distance from the vertex. Find the value of k ?
A1/2B1/3C2/3D1The angle made by a double ordinate of length 8a at the vertex of the parabola y2=4ax is
Aπ/3Bπ/2Cπ/4Dπ/6If a focal chord of the parabola be at a distanced from the vertex, then its length is equal to
A2a2dBa2d2C4a3d2Dd2a
Find the angle made by a double ordinate of length 2a at the vertex of the parabola y2=ax.
View SolutionFind the area cut off from the parabola 2y=3x2 by the line 2y=3x+12.
View SolutionFind the angle made by a double ordinate of length 8a at the vertex of the parabola y2=4ax.
View SolutionSquare of the distance of the point from x-axis is double of its distance from the origin.
View SolutionIf the sum of the squares of the distances of a point from the three coordinate axes be 36, then its distance from the origin is :
View Solution