Find the area contained between the two arms of curves ${(y - x)}^{2} = x^{5}$ between $x = 0$ and $x = 1$ .

Video Solution

Text Solution

Verified by Experts

${(y - x)}^{2} = x^{5} \Rightarrow y = x \pm x^{5 / 2}$
For arm
$y = x + x^{5 / 2} \Rightarrow \frac{d y}{d x} = 1 + \frac{5}{2} x^{3 / 2} > 0 x \geq 0$ .

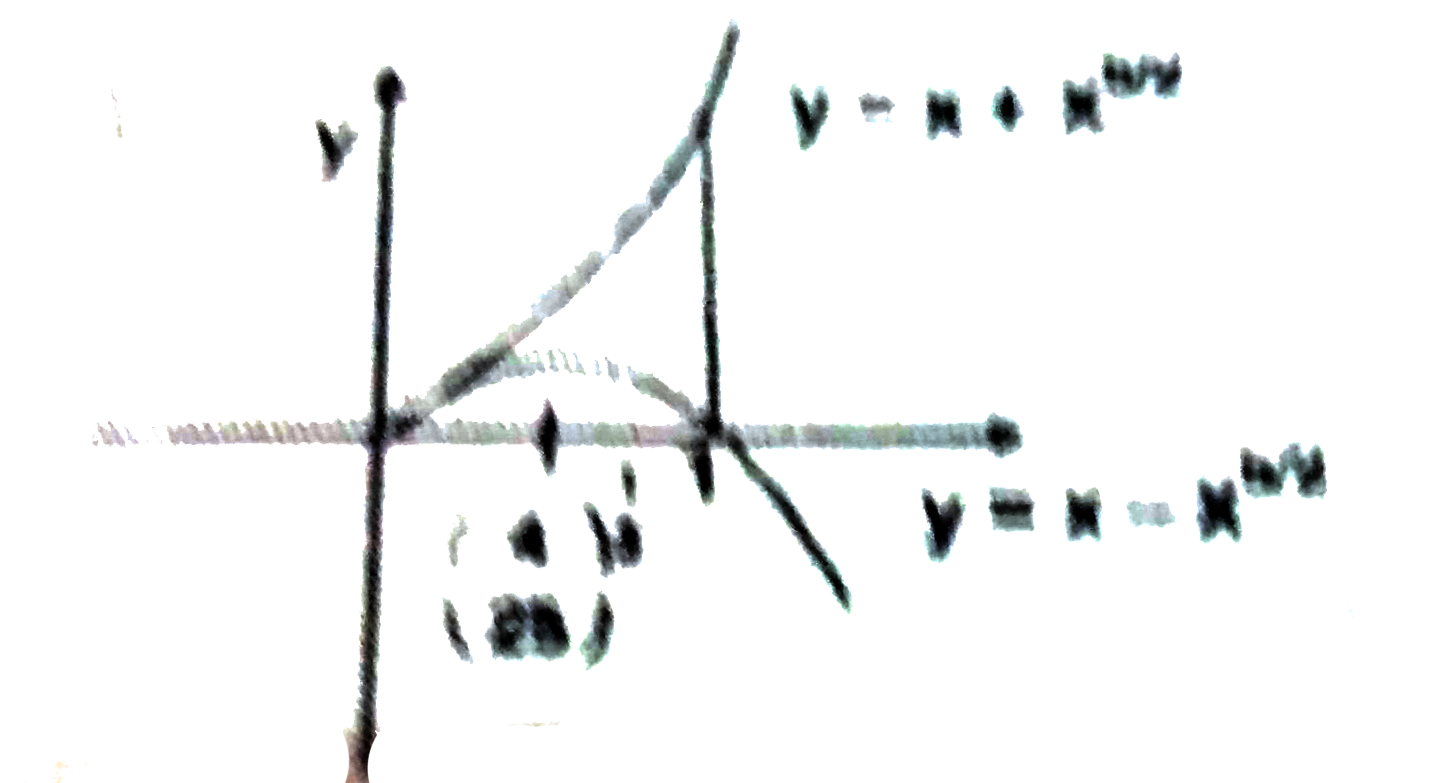
y is incresing function.
For arm,
$y = x - x^{5 / 2} \Rightarrow \frac{d y}{d x} = 1 - \frac{5}{2} x^{32}$
$\frac{5}{2} = 0 \Rightarrow x = {(\frac{4}{25})}^{1 / 2}, \frac{d^{2} y}{{d x}^{2}} = - \frac{5}{4} x^{\frac{1}{2}} < 0$ at $x = {(\frac{4}{25})}^{1 / 3}$
$∴$ at $x = {(\frac{4}{25})}^{1 / 3}$ , $y = x - x^{5 / 2}$ has maxima.
Required area $= 1 \int 0 (x + x^{5 / 2} - x + x^{5 / 2}) d x = 2 1 \int 0 x^{5 / 2} d x = {[\frac{2 x^{7 / 2}}{7 / 2}]}_{0}^{1} = \frac{4}{7}$

Updated on:21/07/2023

The area contained between the x-axis and one area of the curve $y = cos 3 x,$ is
A $1 / 3$
B $2 / 3$
C $2 / 7$
D $2 / 5$
The area enclosed between the curves $y^{2} = x and y = | x |$ is :
A $2 / 3$
B1
C $1 / 6$
D $1 / 3$
The area between the arms of the curve $| y | = x^{3}$ from $x = 0$ to $x = 2$ is
A2
B4
C8
D16