If the area bounded by f(x)=sqrt(tan x), y=f(c), x=0 and x=a, 0ltcltal

Class 12 MATHS DEFINITE INTEGRAL

Topper's Solved these Questions

DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCECHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Exercise 1 Part-II
55 Videos
DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCECHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Exercise 1 Part-III
2 Videos
DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCECHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Self practive problem
56 Videos
COMBINATORICSBOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
8 Videos
DPPBOOK - RESONANCECHAPTER - DPPEXERCISE - QUESTION
665 Videos

Knowledge Check

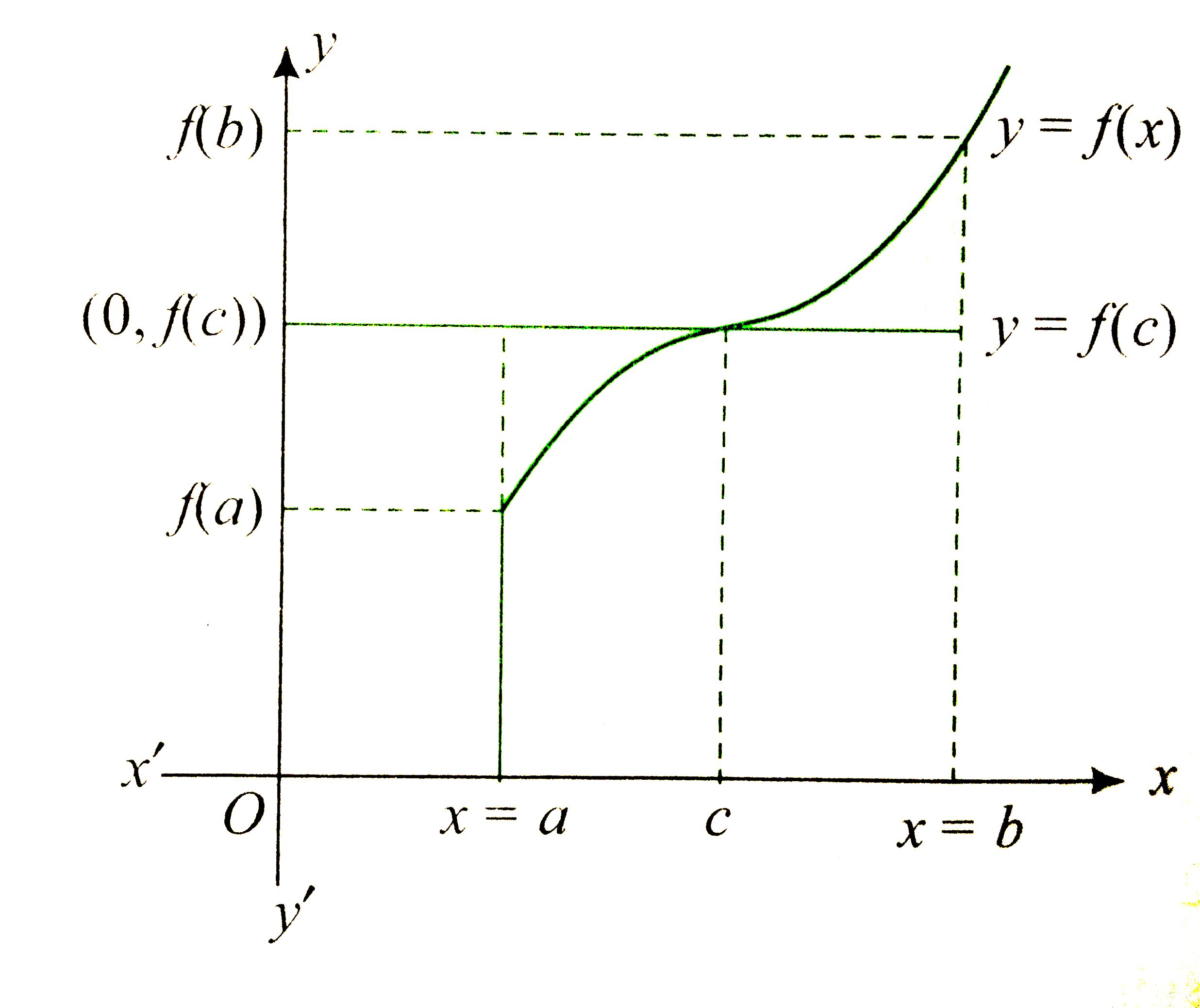
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at $x = a, x = b, y = f (x) and y = f (c) (where c \in (a, b)) is minimum when c = \frac{a + b}{2}$ .
$Proof : A = \int_{a}^{c} (f (c) - f (x)) d x + \int_{c}^{b} (f (c)) d x$
$= f (c) (c - a) - \int_{a}^{c} (f (x)) d x + \int_{a}^{b} (f (x)) d x - f (c) (b - c)$
$\Rightarrow A = [2 c - (a + b)] f (c) + \int_{c}^{b} (f (x)) d x - \int_{a}^{c} (f (x)) d x$

Differentiating w.r.t. c, we get
$\frac{d A}{d c} = [2 c - (a + b)] f' (c) + 2 f (c) + 0 - f (c) - (f (c) - 0)$
For maxima and minima , $\frac{d A}{d c} = 0$
$\Rightarrow f' (c) [2 c - (a + b)] = 0 (a s f' (c) \neq 0)$
Hence, $c = \frac{a + b}{2}$
$Also for c < \frac{a + b}{2}, \frac{d A}{d c} < 0 and for c > \frac{a + b}{2}, \frac{d A}{d c} > 0$
Hence, A is minimum when $c = \frac{a + b}{2}$ .
If the area bounded by $f (x) = \frac{x^{3}}{3} - x^{2} + a$ and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
A $1 / 2$
B2
C1
D $2 / 3$
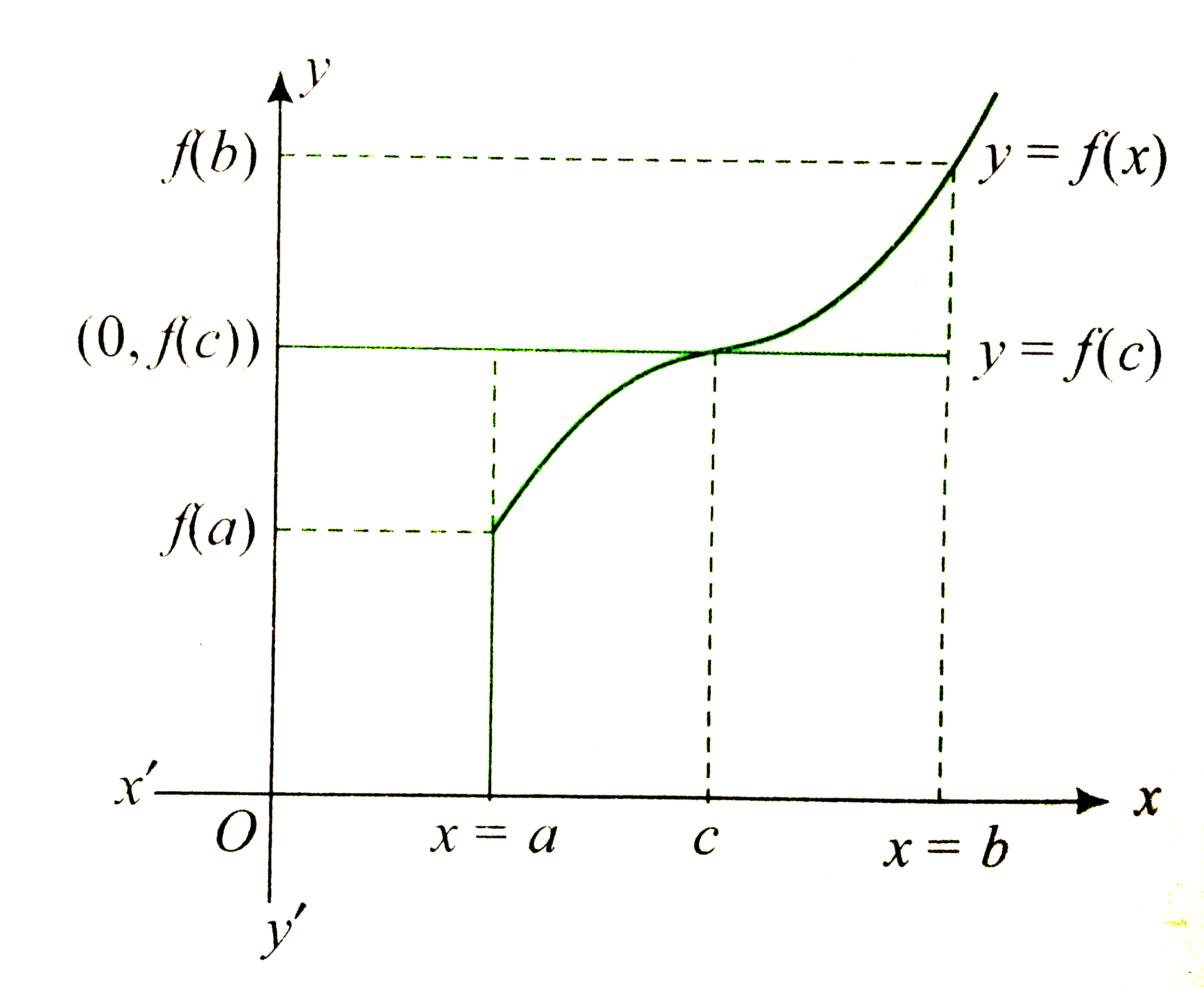
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at $x = a, x = b, y = f (x) and y = f (c) (where c \in (a, b)) is minimum when c = \frac{a + b}{2}$ .
$Proof : A = \int_{a}^{c} (f (c) - f (x)) d x + \int_{c}^{b} (f (c)) d x$
$= f (c) (c - a) - \int_{a}^{c} (f (x)) d x + \int_{a}^{b} (f (x)) d x - f (c) (b - c)$
$\Rightarrow A = [2 c - (a + b)] f (c) + \int_{c}^{b} (f (x)) d x - \int_{a}^{c} (f (x)) d x$

Differentiating w.r.t. c, we get
$\frac{d A}{d c} = [2 c - (a + b)] f' (c) + 2 f (c) + 0 - f (c) - (f (c) - 0)$
For maxima and minima , $\frac{d A}{d c} = 0$
$\Rightarrow f' (c) [2 c - (a + b)] = 0 (a s f' (c) \neq 0)$
Hence, $c = \frac{a + b}{2}$
$Also for c < \frac{a + b}{2}, \frac{d A}{d c} < 0 and for c > \frac{a + b}{2}, \frac{d A}{d c} > 0$
Hence, A is minimum when $c = \frac{a + b}{2}$ .
If the area enclosed by $f (x) = sin x + cos x, y = a$ between two consecutive points of extremum is minimum, then the value of a is
A0
B-1
C1
D2

If the area bounded by $f (x) = \sqrt{tan x}, y = f (c), x = 0 and x = a, 0 < c < a < \frac{π}{2}$ is minimum then find the value of c.

The correct Answer is: $4$ sq. units

Topper's Solved these Questions

Similar Questions

Knowledge Check

RESONANCE-DEFINITE INTEGRATION & ITS APPLICATION -Exercise 1

If the area bounded by f(x)=√tanx,y=f(c),x=0andx=a,0<c<a<π2 is minimum then find the value of c.

The correct Answer is:4 sq. units

Topper's Solved these Questions

Similar Questions

Knowledge Check

RESONANCE-DEFINITE INTEGRATION & ITS APPLICATION -Exercise 1

If the area bounded by $f (x) = \sqrt{tan x}, y = f (c), x = 0 and x = a, 0 < c < a < \frac{π}{2}$ is minimum then find the value of c.

The correct Answer is: $4$ sq. units