Let g(t)=x2∫x1f(t,x)dx. Then g'(t)=x2∫x1∂∂t(f(t,x))dx, Consider f(x)=π∫0ln(1+xcosθ)cosθdθ.
The number of critical point of f(x), in the interior of its domain, is
discontinuous at x=0
differentiable at x=1
continuous at x=0
none of these
The correct Answer is:B, C
Step by step video, text & image solution for Let g(t) = underset(x_(1))overset(x_(2))intf(t,x) dx. Then g'(t) = underset(x_(1))overset(x_(2))int(del)/(delt) (f(t,x))dx, Consider f(x) = underset(0)overset(pi)int (ln(1+xcostheta))/(costheta) d theta. The number of critical point of f(x), in the interior of its domain, is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Exercise 3 Part - I50videos
DEFINITE INTEGRATION & ITS APPLICATION
- BOOK - RESONANCECHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Exercise 3 Part - II25videos
DEFINITE INTEGRATION & ITS APPLICATION
- BOOK - RESONANCECHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Exercise 2 Part - III30videos
DEFINITE INTEGRATION & ITS APPLICATION
- BOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)8videos
COMBINATORICS
- BOOK - RESONANCECHAPTER - DPPEXERCISE - QUESTION665videos
DPP
Similar Questions
Knowledge Check
- Question 1 - Select One
Let g(t)=∫x2x1f(t,x)dx. Then g'(t)=∫x2x1∂∂t(f(t,x))dx, Consider f(x)=∫π0ln(1+xcosθ)cosθdθ.
The number of critical point of f(x), in the interior of its domain, isA0B1C2Dinfinitely many - Question 2 - Select One
2∫13x2dx=???
A9B7Cx3+6D3 - Question 3 - Select One
f(x)=xt−10(t−2)2(t−4)5dt(x>0) then numb er of points of extremum of f(x) is
A4B3C2D1
Let LimT→∞1TT∫0(sinx+sinax)2dx=L then
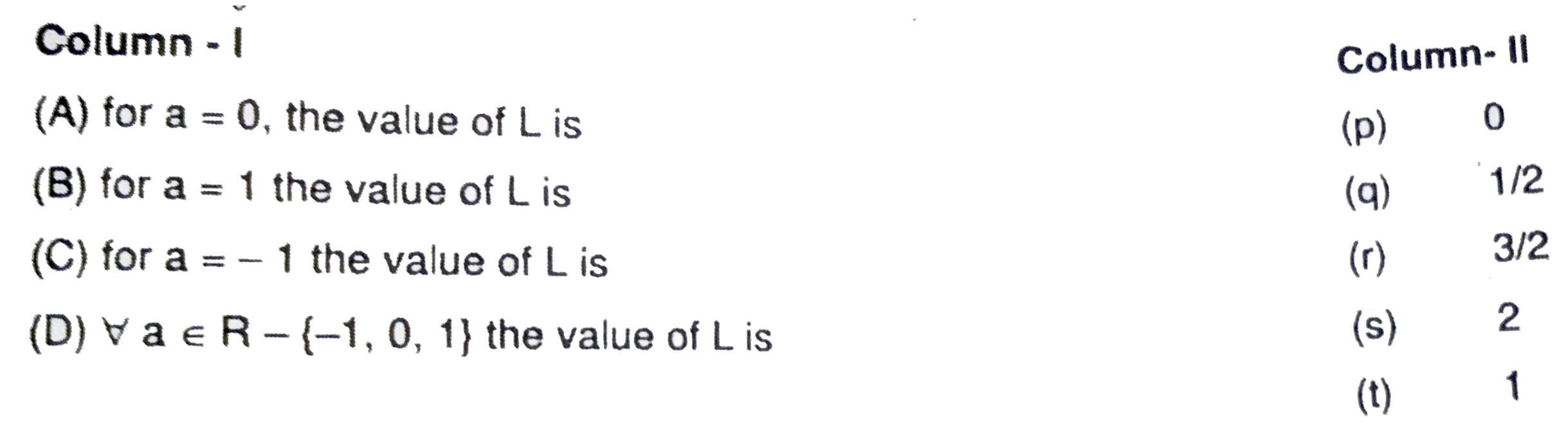 View Solution
View SolutionThe number of critical points of the functionf(x)=∫x0et(t−1)(t−2)(t−3)dt
View SolutionFor x∈(0,5π2) define
f(x) = x∫0√tsintdt
Then has :View SolutionLet A=[2 q0 1]andA8=[x yq0 1], then x-y is -
View SolutionIf ∫1000f(x)dx=a, then 100∑r=1⎛⎜⎝1∫0f(r−1+x)dx⎞⎟⎠=
View Solution

