Question

(i) Determine whether $f\left(x\right)=\frac{2x+3}{4}$ for $f:R\to R$ is invertible or not If so find it.
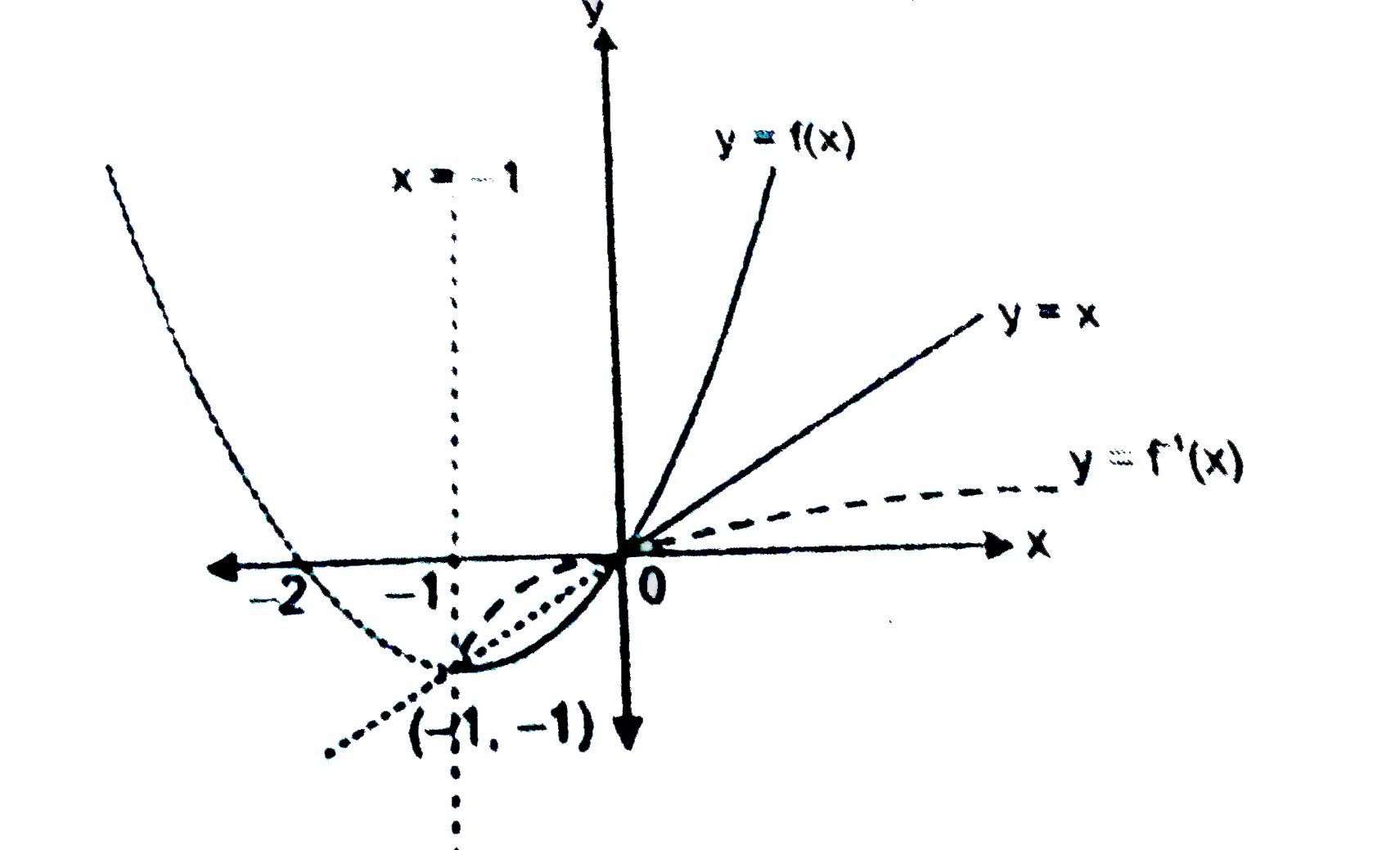
(ii) Let $f\left(x\right)=x^2+2x,x\ge -1$ . Draw graph of $f^{-1}\left(x\right)$ also find the number of solutions of the equation $f\left(x\right)=f^{-1}\left(x\right)$
(iii) If $y=f\left(x\right)=x^2-3x+2,x\le 1$.Find the value of $g\text{'}\left(2\right)$ where $g$ is inverse of $f$

Explanation

(i) Given functions is one -one and otno, therefore it is invertible,
`y=(2x+3)/4impliesx+(4y-3)/2:.f^(-1)(x)=(4x-3)/2`
(ii) `f(x)=f^(-1)(x)` is equivalent to `f(x)=ximpliesx^(2)+2x=ximpliesx(x+1)=0impliesx=0,-1`
Hence two solution for `f(x)=f^(-1)(x)`

(iii) `f(x)=x^(2)-3x+2,xle1`
`fg(x)=g(x)^(2)-3g(x)+2`
`implies2=g(2)^(2)-3g(2)+2`
`impliesg(2)=0,3le1`
so `g(2)=0`
`f'(x)=2x-3`
`fg(x)=ximpliesf'(g(x)).g'(x)=1impliesg'(2)=1/(f'(g(2)))=1/(f'(0))=-1/3`