If the graph of the function y = f(x) is symmetrical about the line x = 2, then
A
f(x+2)=f(x−2)
B
f(2+x)=f(2−x)
C
f(x)=f(−x)
D
f(x)=−f(−x)
Video Solution
Text Solution
The correct Answer is:B
NA
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - INTEGER_TYPE21videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - MCQ_TYPE31videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - MATCH THE COLUMN5videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)4videos
NUMBER THEORY
- BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)3videos
SEQUENCE & SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
If the graph of a function f(x is symmetrical about the line x = a, then
Af(a+x)=f(a−x)Bf(a+x)=f(x−a)Cf(x)=f(−x)Dnone of these - Question 2 - Select One
If the garph of the function f(x)=ax3+x2+bx+c is symmetric about the line x = 2, then the value of a+b is equal to
A10B−4C16D−10 - Question 3 - Select One
If the function f(x) is symmetric about the line x=3, then the value of the integral I=∫8−2f(x)f(x)+f(6−x)dx is
A0B5C10D16
If the graph of y=f(x) is symmetrical about the lines x=1andx=2, then which of the following is true? (a)f(x+1)=f(x) (b) f(x+3)=f(x) (c)f(x+2)=f(x) (d) None of these
View SolutionIf the graph of the function
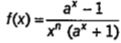 is symmetric about y-axis, then n is equal to :View Solution
is symmetric about y-axis, then n is equal to :View SolutionThe graph of the function f(x)=−2−|x|
View SolutionIf f(x)=f(2a−x) then the graph of f(x) is symmetric about the line
View SolutionIf the graph of y=ax3+bx2+cx+d is symmetric about the line x=K then the value of a+K is (y is not a constant function)
View Solution

