If the graph of the function f(x)=ax−1xn(ax+1) is symmetric about y-axis then n is equal to
1/5
1/3
1/4
−1/3
The correct Answer is:A, B, D
To determine the value of n such that the function
f(x)=ax−1xn(ax+1)
is symmetric about the y-axis, we need to check the condition for even functions. A function is symmetric about the y-axis if f(−x)=f(x).
1. Find f(−x):
Substitute −x into the function:
f(−x)=a−x−1(−x)n(a−x+1)
2. Simplify f(−x):
We can rewrite a−x as 1ax:
f(−x)=1ax−1(−x)n(1ax+1)=1−axax(−x)n(1+axax)
Simplifying further:
f(−x)=1−ax(−x)n(1+ax)
3. Rearranging f(−x):
We can express (−x)n as (−1)nxn:
f(−x)=1−ax(−1)nxn(1+ax)
4. Set f(−x) equal to f(x):
We need to equate f(−x) and f(x):
1−ax(−1)nxn(1+ax)=ax−1xn(ax+1)
5. Cross-multiply to eliminate fractions:
Cross-multiplying gives:
(1−ax)(xn(ax+1))=(ax−1)(−1)nxn(1+ax)
6. Simplify both sides:
The left side becomes:
xn(1−ax)(ax+1)=xn(ax+1−a2x−ax)=xn(1−a2x)
The right side simplifies to:
(−1)nxn(ax−1)(1+ax)=(−1)nxn(a2x−1)
7. Equate the simplified forms:
Now we have:
xn(1−a2x)=(−1)nxn(a2x−1)
8. Divide both sides by xn (assuming x≠0):
1−a2x=(−1)n(a2x−1)
9. Rearranging gives:
1−a2x=(−1)na2x−(−1)n
Rearranging this leads to:
1+(−1)n=a2x(1+(−1)n)
10. Analyze the equation:
For this equation to hold for all x, the term 1+(−1)n must equal zero, which implies that n must be odd.
Conclusion:
Thus, the value of n must be an odd integer.
Substitute −x into the function:
f(−x)=a−x−1(−x)n(a−x+1)
We can rewrite a−x as 1ax:
f(−x)=1ax−1(−x)n(1ax+1)=1−axax(−x)n(1+axax)
Simplifying further:
f(−x)=1−ax(−x)n(1+ax)
We can express (−x)n as (−1)nxn:
f(−x)=1−ax(−1)nxn(1+ax)
We need to equate f(−x) and f(x):
1−ax(−1)nxn(1+ax)=ax−1xn(ax+1)
Cross-multiplying gives:
(1−ax)(xn(ax+1))=(ax−1)(−1)nxn(1+ax)
The left side becomes:
xn(1−ax)(ax+1)=xn(ax+1−a2x−ax)=xn(1−a2x)
The right side simplifies to:
(−1)nxn(ax−1)(1+ax)=(−1)nxn(a2x−1)
Now we have:
xn(1−a2x)=(−1)nxn(a2x−1)
1−a2x=(−1)n(a2x−1)
1−a2x=(−1)na2x−(−1)n
Rearranging this leads to:
1+(−1)n=a2x(1+(−1)n)
For this equation to hold for all x, the term 1+(−1)n must equal zero, which implies that n must be odd.
Thus, the value of n must be an odd integer.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - COMPREHENSION_TYPE6videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - JEE ADVANCED14videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - RELATION, FUNCTION & ITFEXERCISE - INTEGER_TYPE21videos
RELATION, FUNCTION & ITF
- BOOK - RESONANCECHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)4videos
NUMBER THEORY
- BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)3videos
SEQUENCE & SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph of the function y=loga(x+√x2+1) is not symmetric about the origin.
ATrueBFalseCCan't sayDInsufficient data - Question 2 - Select One
If the real valued function f(x)=ax−1xn(ax+1) is even, then n is equal to
A2B44257C44287D3 - Question 3 - Select One
If the real valued function f(x)=ax−1xn(ax+1) is even, then n is equal to
A2B44257C44287D3
If the graph of the function
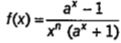 is symmetric about y-axis, then n is equal to :View Solution
is symmetric about y-axis, then n is equal to :View SolutionIf the graph of the function y = f(x) is symmetrical about the line x = 2, then
View SolutionLet f(x)=√x4+15, then the gragh of the function y=f(x) is symmetrical about
View SolutionThe graph of the function y=f(x) is symmetrical about the line x=2, then :
View SolutionThe graph of the function y=f(x) is symmetrical about the line x=2, then :
View Solution

