Consider a simple RC circuit as shown in figure 1.
Process 1 : In the circuit the switch S is closed at t=0 and the capacitor if fully charged to voltage V0 (i.e., charging continues for time T>>RC). In the process some dissipation (ED) occurs across the resistance R. The amount of energy finally stored in the fully charged capacitor is Ec.
Process 2 : In a different process the voltage is first set to V03 and maintained for a charging time T>>RC. Then the voltage is raised to 2C03 without discharging the capacitor and again maintained for a time T>>RC. The process is repeated one more time by raising the voltage to V0 and the capacitor is charged to the same final voltage V0 as in Process 1.
These two processes are depicted in figure 2.
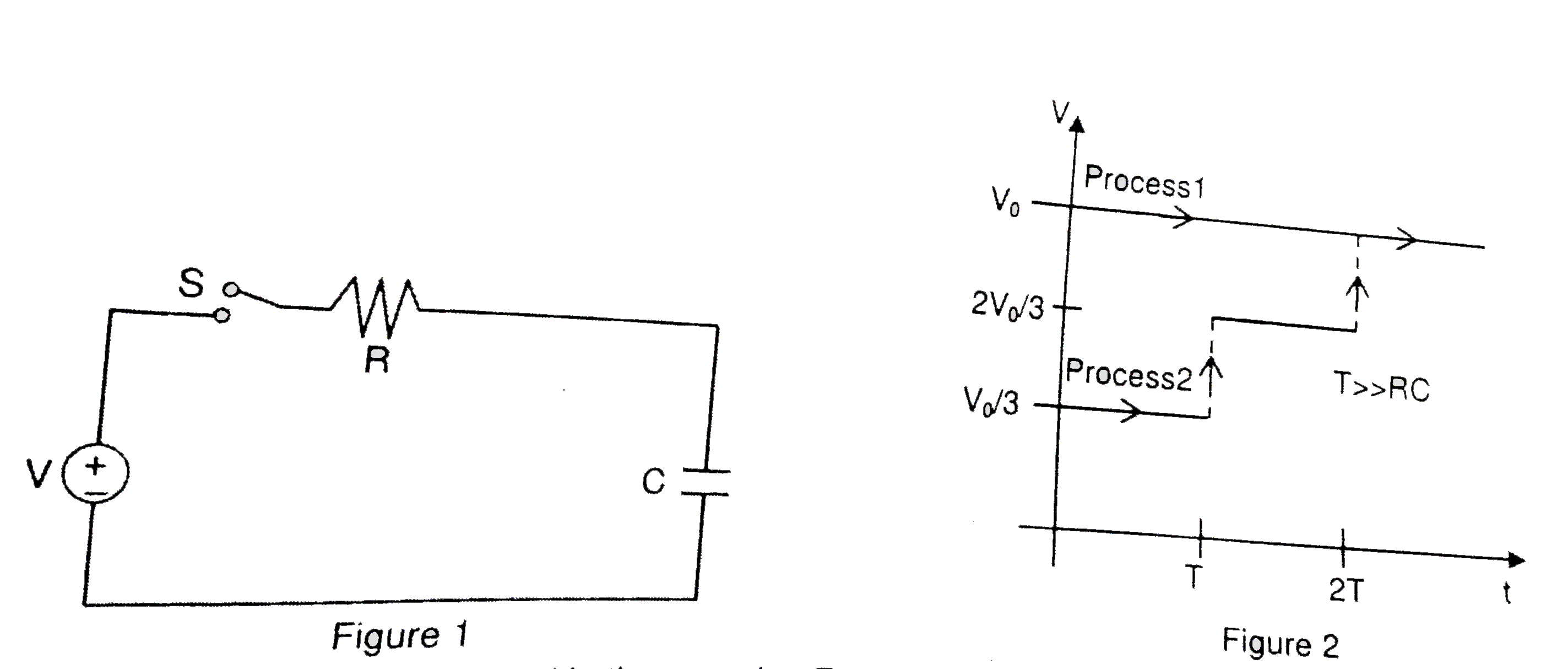
In process 1, the energy stored in the capacitor Ec and heat dissipated across resistance ED are related by :
Ec=12ED
Ec=EDln 2
Ec=2ED
Ec=ED
The correct Answer is:D
Topper's Solved these Questions
- CAPACITANCEBook:RESONANCEChapter:CAPACITANCEExercise:High Level Problems
Explore 16 Videos
- CAPACITANCEBook:RESONANCEChapter:CAPACITANCEExercise:Exercise - 2
Explore 74 Videos
- ATOMIC PHYSICSBook:RESONANCEChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
- COMMUNICATION SYSTEMSBook:RESONANCEChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
Similar Questions
Process 1 : In the circuit the switch S is closed at and the capacitor is fully charged to voltage v0 (i.e., charging continues for time T >> RC). In the process some dissipation (ED) occurs across the resistance R. The amount of energy finally stored in the fully charged capacitor is EC.
Process 2 : In a different process the voltage is first set to v03 maintained for a charging time T >> RC. Then the voltage is raised to 2V03 without discharging the capacitor and again maintained for a time T >> RC. The process is repeated one more time by raising the voltage to v0 and the capacitor is charged to the same final voltage v0 as in process 1. These two processes are depicted in Figure 2.
In Process 2, total energy dissipated across the resistance ED is :
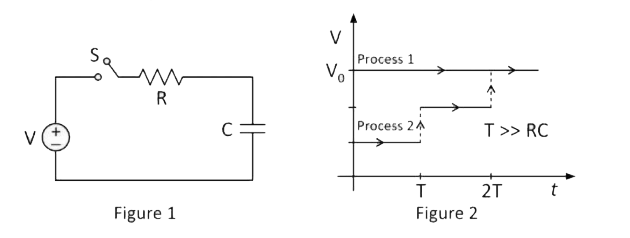
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
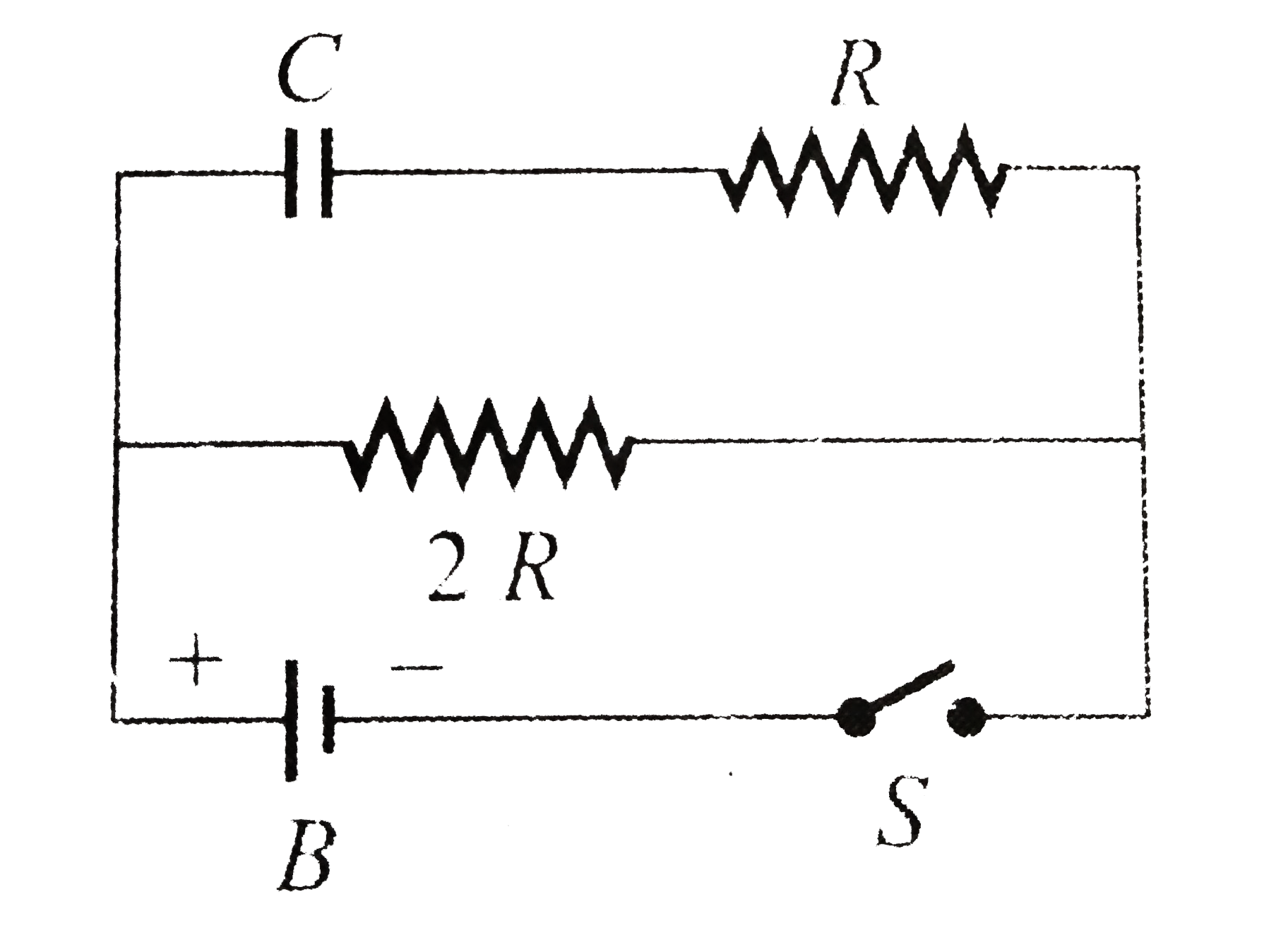
View Solution
Knowledge Check
Consider a simple RC circuit as shown in figure 1.
Process 1 : In the circuit the switch S is closed at t=0 and the capacitor if fully charged to voltage V0 (i.e., charging continues for time T>>RC). In the process some dissipation (ED) occurs across the resistance R. The amount of energy finally stored in the fully charged capacitor is Ec.
Process 2 : In a different process the voltage is first set to V03 and maintained for a charging time T>>RC. Then the voltage is raised to 2C03 without discharging the capacitor and again maintained for a time T>>RC. The process is repeated one more time by raising the voltage to V0 and the capacitor is charged to the same final voltage V0 as in Process 1.
These two processes are depicted in figure 2.
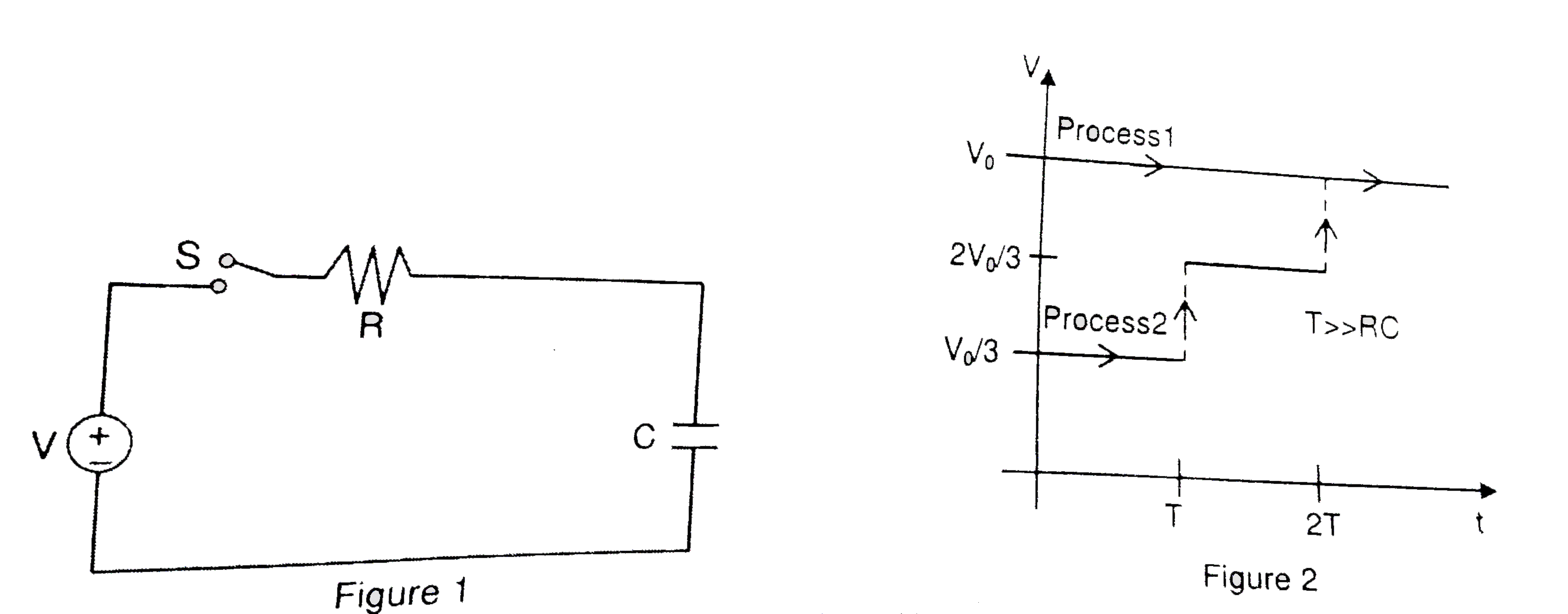
In process 2, total energy dissipated across the resistance ED is :AED=3(12CV20)BED=13(12CV20)CED=3CV20DED=12CV20In the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
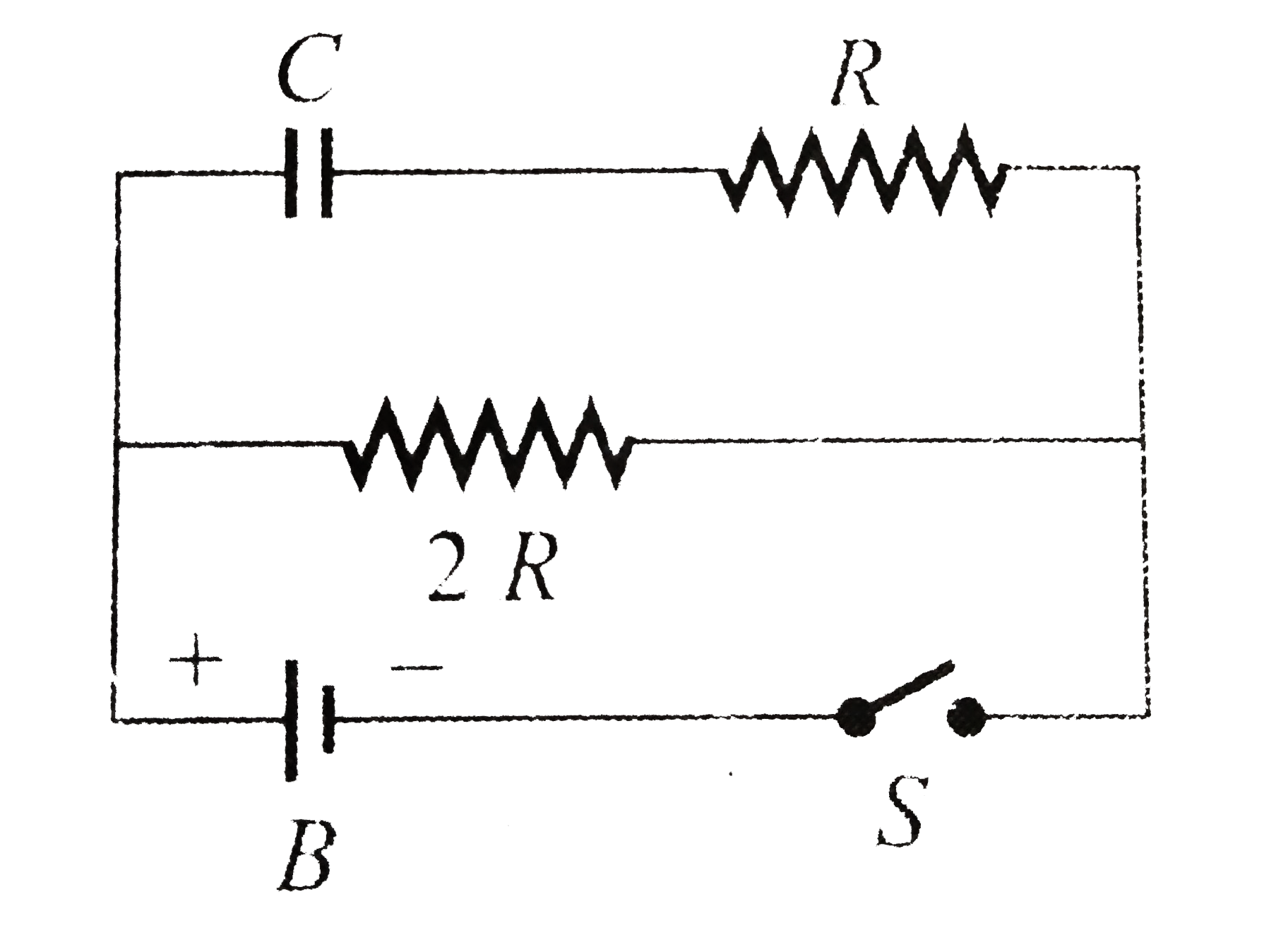 ARCB3RCC23RCDRCIn(23)
ARCB3RCC23RCDRCIn(23)In given circuit, switch S is closed at t=0 . The charge on the capacitor ar steady state will be
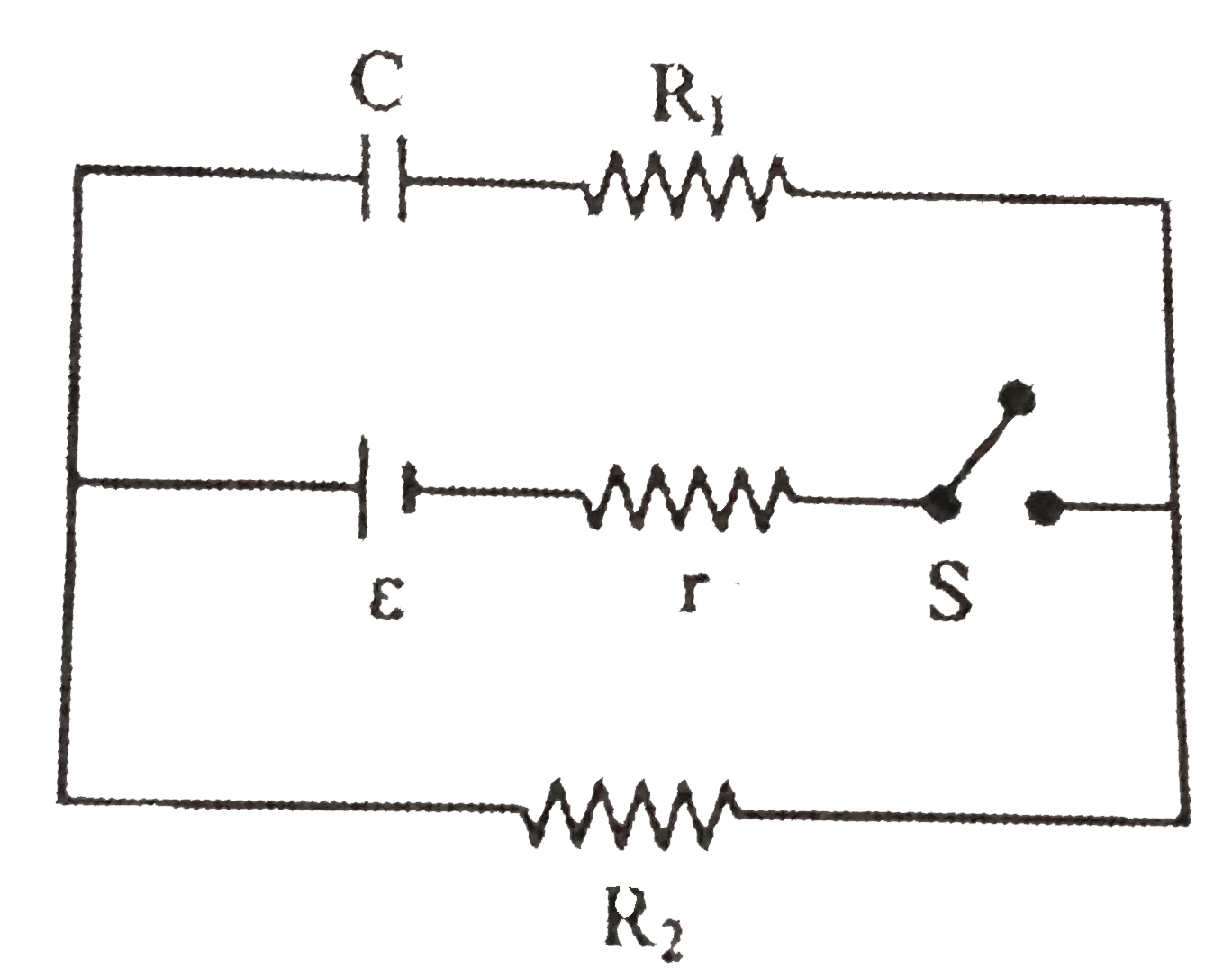 ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2
ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2
In the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is
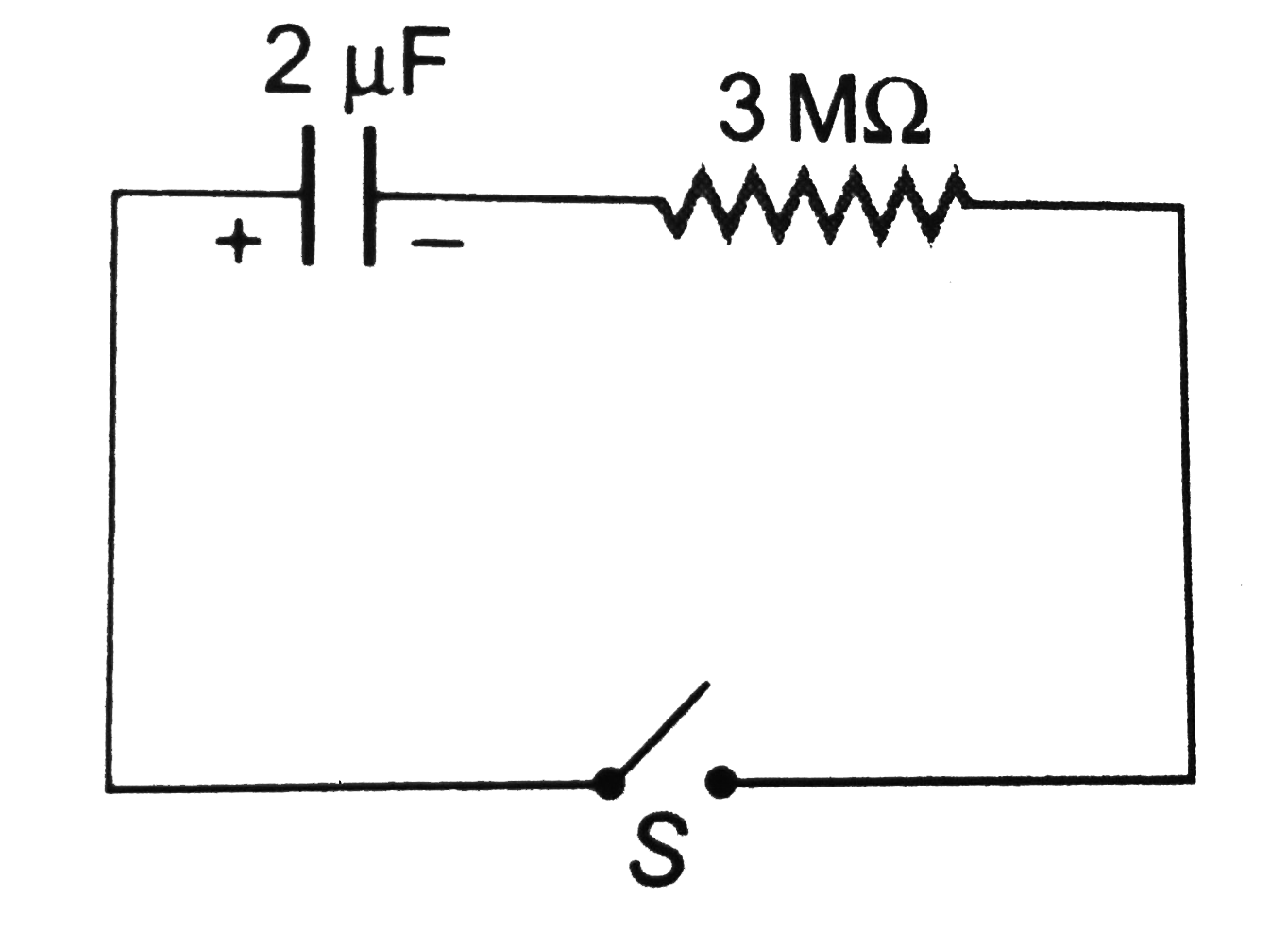
View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
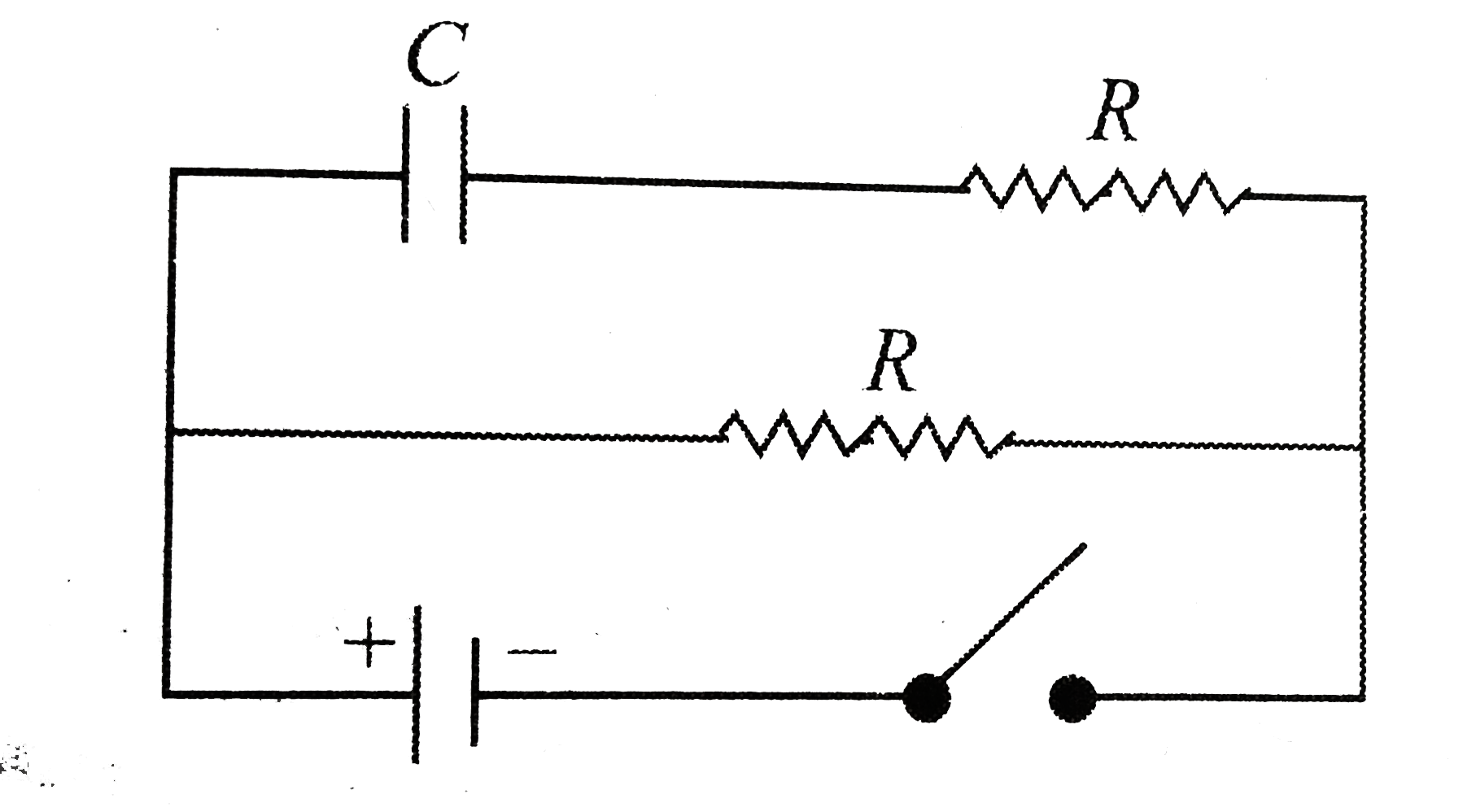
View SolutionConsider the circuit shown in the figure below :
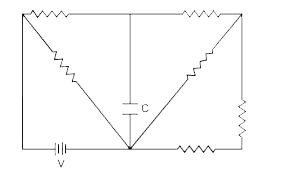
All the resistors are identical. The charge stored in the capacitor, once it is fully charged, is
View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is

View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant

View Solution
