A cylindrical conductor has length l and area of cross section A. Its conductivity changes with distance (x) from one of its ends as σ=σ0lx.[σ0is a constant]. Calculate electric field inside the conductor as a function of x, when a cell of emf V is connected across the ends.
The electric resistance of cylinder along its axis is l2σ0A
The electric current in the wire will be V0σ0A2l
The electric current in the wire will be 2V0σ0l
The electric field in the wire at x in xylinder will be 2V0l2x
The correct Answer is:A, C, D
Step by step video, text & image solution for A cylindrical conductor has length l and area of cross section A. Its conductivity changes with distance (x) from one of its ends as sigma = sigma_(0) (l)/(x). [sigma_(0) "is a constant"]. Calculate electric field inside the conductor as a function of x, when a cell of emf V is connected across the ends. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-4)12videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-1)22videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-2)16videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.711videos
DAILY PRACTICE PROBLEM
Similar Questions
A cylindrical conductor of length l and radius a has conductivity near its axis as σ. The conductivity of material increases linearly with the distance from axis and becomes 2σ near the surface.The resistance of conductor for longitudinal current is
View SolutionA conductor of length l, area of cross section A and resistivity ρ has resistance = R. It is connected across a cell of voltage V . What will be the current flowing resistor if its length is doubled and cross section area is halved.
View Solution
Knowledge Check
- Question 1 - Select One
A conductor of length l and area of cross-section A has a resistance R then its specific resistance is
Aρ=RAlBρ=RAlCρ=lRADρ=R2Al - Question 2 - Select One
A cylindrical conductor of length l and uniform area of cross section A has resistance R. Another conductor of length 2.5l and resistance 0.5R of the same material has an area of cross section
A5AB2.5AC0.5AD15A - Question 3 - Select One or More
A cylindrical conductor AB of length l and area of cross-section a is connected to a battery having emf E and negligible internal resistance. The specific conductivity of cylindrical conductor varies as σ=σ01√x, where σ0 is constant and x is distance from end A. What is the electric field just near the end B of cylinder?
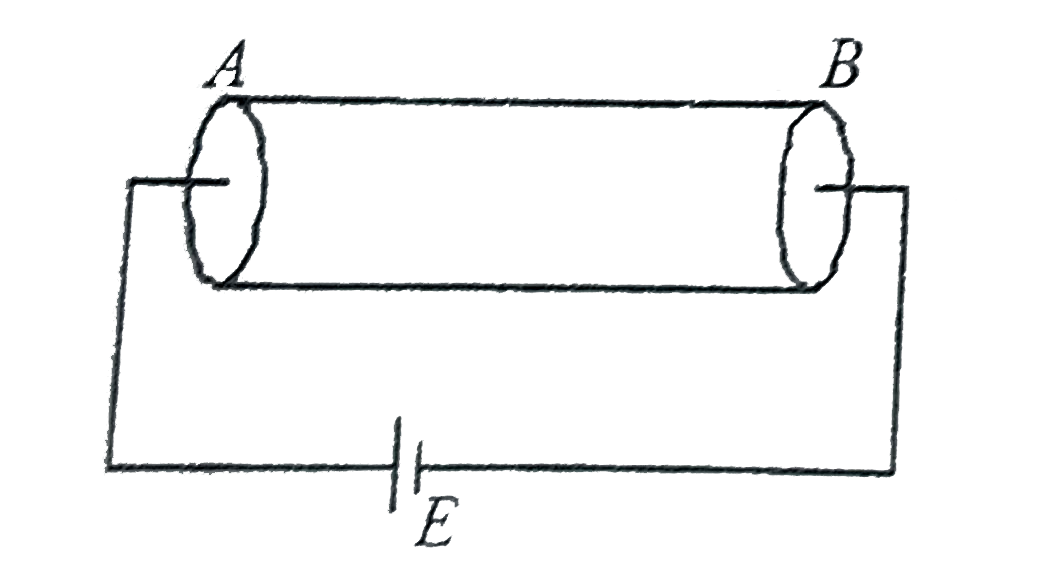 AElB3E2lC2E3lDE2l
AElB3E2lC2E3lDE2l
The resistance of wire of length l and area of cross-section a is x ohm. If the wire is stretched to double its length, its resistance would become:
View SolutionA cylindrical conductor has uniform cross-section. Resistivity of its material increase linearly from left end to right end. If a constant current is flowing through it and at a section distance x from left end, magnitude of electric field intensity is E , which of the following graphs is correct
View SolutionConductor of length l has shape of a semi cylinder of radius R(<<l). Cross section of the conductor is shown in the figure. Thickness of the conductor is (<<R) and conductivity of its material varies with angle θ according to the law σ=σ0cosθ where σ0 is a constant. If a battery of emf ε is connected across its end faces (across the semi-circular cross-sections), the magnetic induction at the mid point O of the axis of the semi-cylinder is :
 View Solution
View SolutionA cylindrical metal wire of length l and cross sections area S , has resistance R , conductance G , conductivity σ and resistivity ρ . Which one of the following expressions for σ is valid
View SolutionA cylindrical conductor has uniform cross-section. Resistivity of its material increase linearly from left end to right end. If a constant current is flowing through it and at a section distance x from left end, magnitude of electric field intensity is E , which of the following graphs is correct
View Solution

