A network of resistance is constructed with R1andR2 as shown in the figure. The potential at the points 1, 2, 3,………., N are V1,V2,V3,……..,Vn respectively each havig a potential K time smaller than privious one. Find :
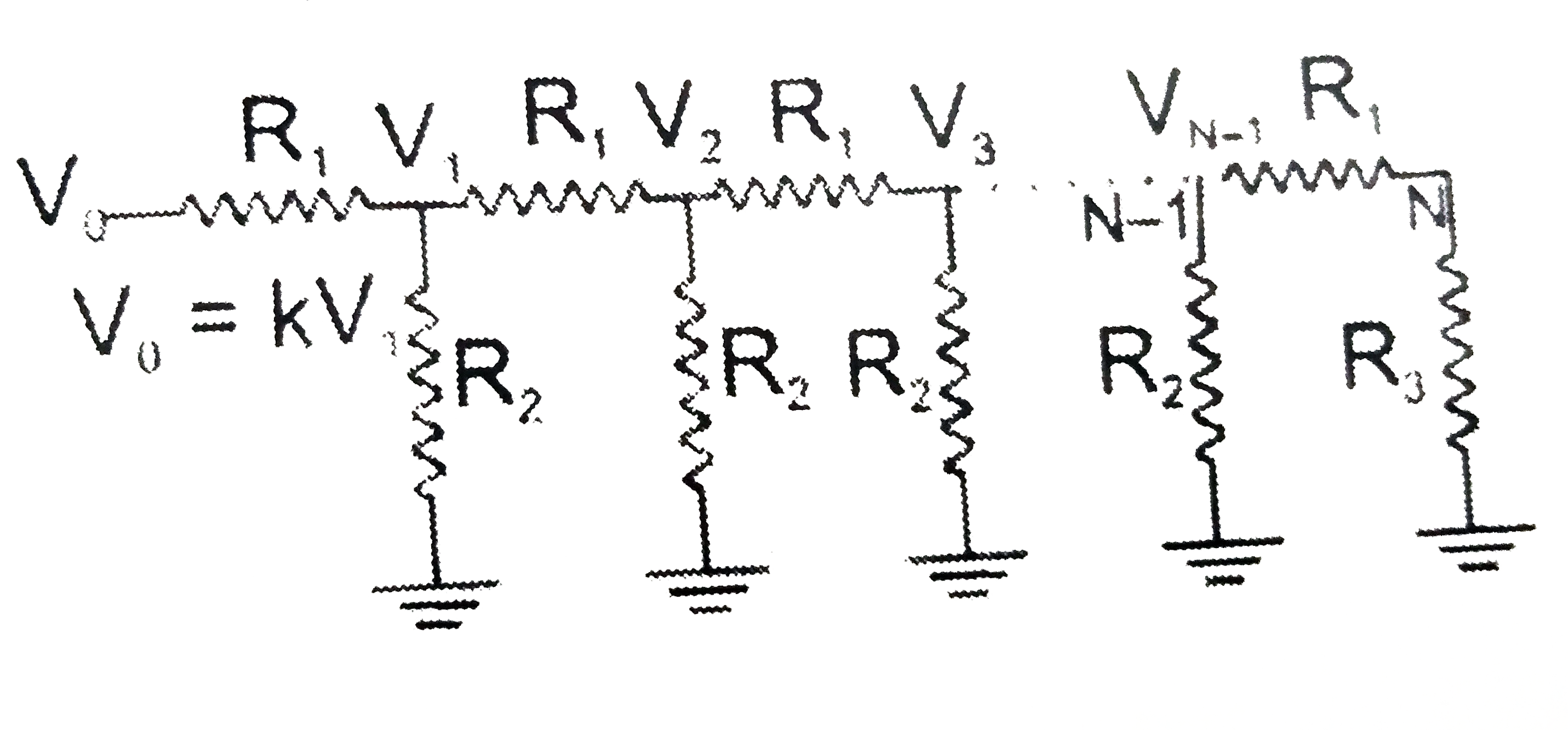
(R1R2)×(R2R3) in terms of K.
K-1
K2−1
1K+1
K−1K+1
The correct Answer is:A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-1)
22 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-2)
23 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-3)
22 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
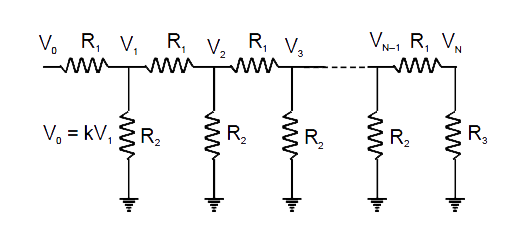
A network of resistance is constructed with R1&R2 as shown in the figure . The potential at the points 1,2,3 ,,,,, N and V1,V2,V3,,,,,,,Vn respectively each having a potential k time smaller than previous one. Find
R1R2andR2R3 in terms of k
View SolutionA network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.
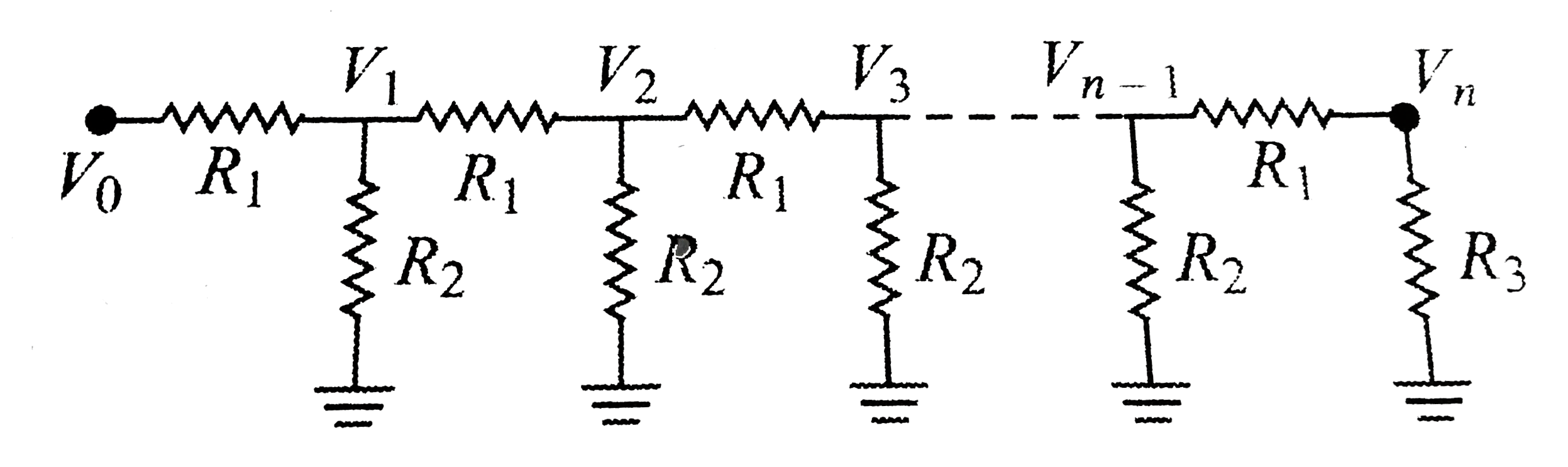
The ratio R1/R2 is
View Solution
Knowledge Check
A network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.
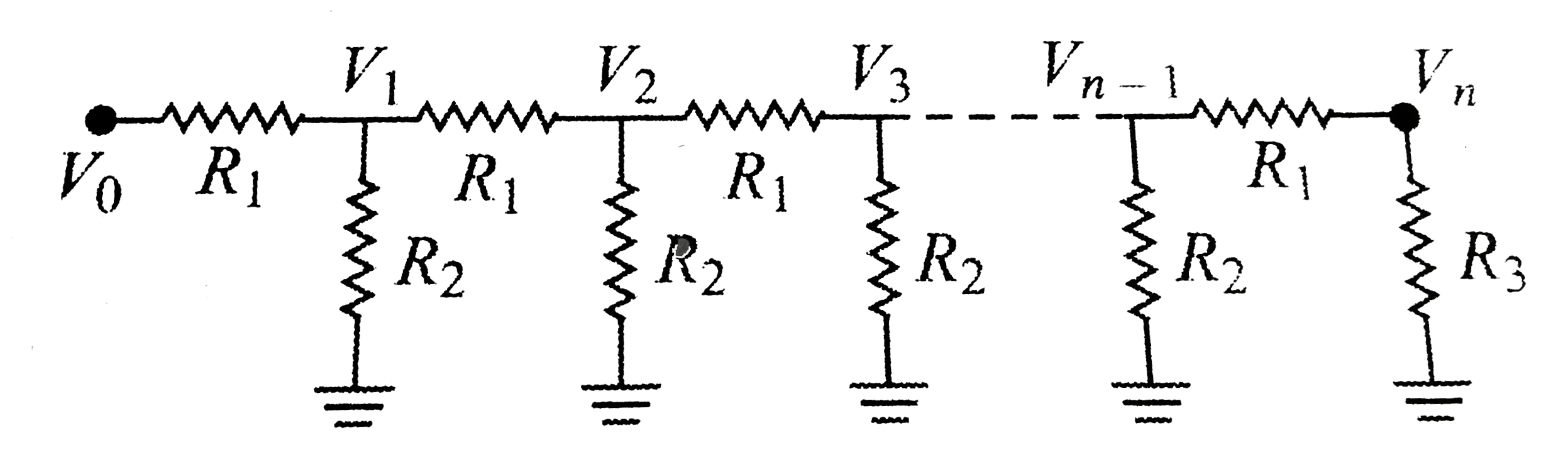
The ratio R2/R3 isA(k−1)2kBk2−1kCkk−1Dk−1k2A network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.

The ratio R1/R2 isAK2−1kBkk−1Ck−1k2D(k−1)2kA network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.

The current that passes through the resistance R2 nearest to the V0 isA(k−1)2kV0R3B(k+1)2k=v0R3C(k+1k2)V0R3D(k−1k2)V0R3
A network of resistance is constructed with R_(1)&R_(2)asshown∈thefigure.Thepotentialatthep∮s1,2,3,,,,,NandV_(1),V_(2),V_(3) ,,,,,,, V_(n)respectivelyeachhav∈gapotentialktimesmal≤rthanpreviouso≠.F∈d<br>currenttˆpassesthroughtheresistanceR_(2)≠arest→theV_(0)∈termsV_(0),k&R_(3).
View SolutionA network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.

The current that passes through the resistance R2 nearest to the V0 is
View SolutionThree capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .
.
View SolutionThree capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .
.
View SolutionTwo satellite are revolving around the earth with velocities v1 and v2 and in radii r1 and r2(r1>r2) respectively. Then
View Solution
