A long solenoid of length l=2.0 m , radius r=0.1 m and total number of turns N=1000 is carrying a current i0=20.0A. The axis of the solenoid conicides with the z-axis.
(a) State the expression for the magnetic field of the solenoid and calculate its value ? Magnetic field.
(b) Obtain the expression for the self - inductance (L) of the solenoid. Calcuate its value. Value of L .
( c) Calculate the energy stored (D) when the solenoid carries this current ?
(d) Let the resistance of the solenoid be R. It is connected to a battery of emf e. Obtain the expression for the current (i) in the solenoid.
(e) Let the solenoid with resistance R describe in part (d) be strecthed at a constant speed u ( l is increased but B and γ are constant ). State kirchhoff's second law for this cases. (Note: Do not solve for the current )
(f) Consider a time varying current i=i0cos(ωt) (where i0=20.0A) flowing in the solenoid. Obtain an expression for the electric field due to the current in the solenoid. (Note: Part(e) is not operative, i.e., the solenoid is not being stretched. )
(g) Consider t=π/2ωandω=200/πrad−s−1 in the previous part. Plot the magnitude of the electric field as a function of the radial distance from the solenoid. Also, sketch the electric lines of force.

N=1000,i0=20A
(a) →B=μ0Nli0(±ˆk)
∣∣→B∣∣=4π×10−3Telsa
(b) ϕ=Li0
BNA=Li0
L=BNAi0=μ0N2πr2l=2π2×10−3H.
(C) E=12Li20=4π210 Joules=3.95J
(d) i=i0(1−e−t/τ)
where τ=LR,i0=εR
(e) ε−iR−ddt(Li)=0 ltbtgt ε−iR−Ldidt−idLdt
ε−iR+Ldidt+idLdt
after time t,
L=μ0N2πr2(l+vt)→dLdt=−μ0N2πr2v(L+vt)2
ε=iR+Ldidt−μ0N2πr2v(L+vt)2
(f) Einduced=∫→E.→dl=−dϕdt
∫→E.→dl=−dϕdt
(d → Radial distance from axis of solenoid :
r→ Radius of solenoid )
For (d<r)
E.2πd=−πd2dBdt
=πd2μ0Nldidt
E.2πd=πd2μ0Nli0ωsin(ωt)
E=μ0Ni0ωdsin(ωt)2l
For d≥r
E.2πd=−π2dBdt
E=μ0Ni0ωr22dlsin(ωt)
(g) 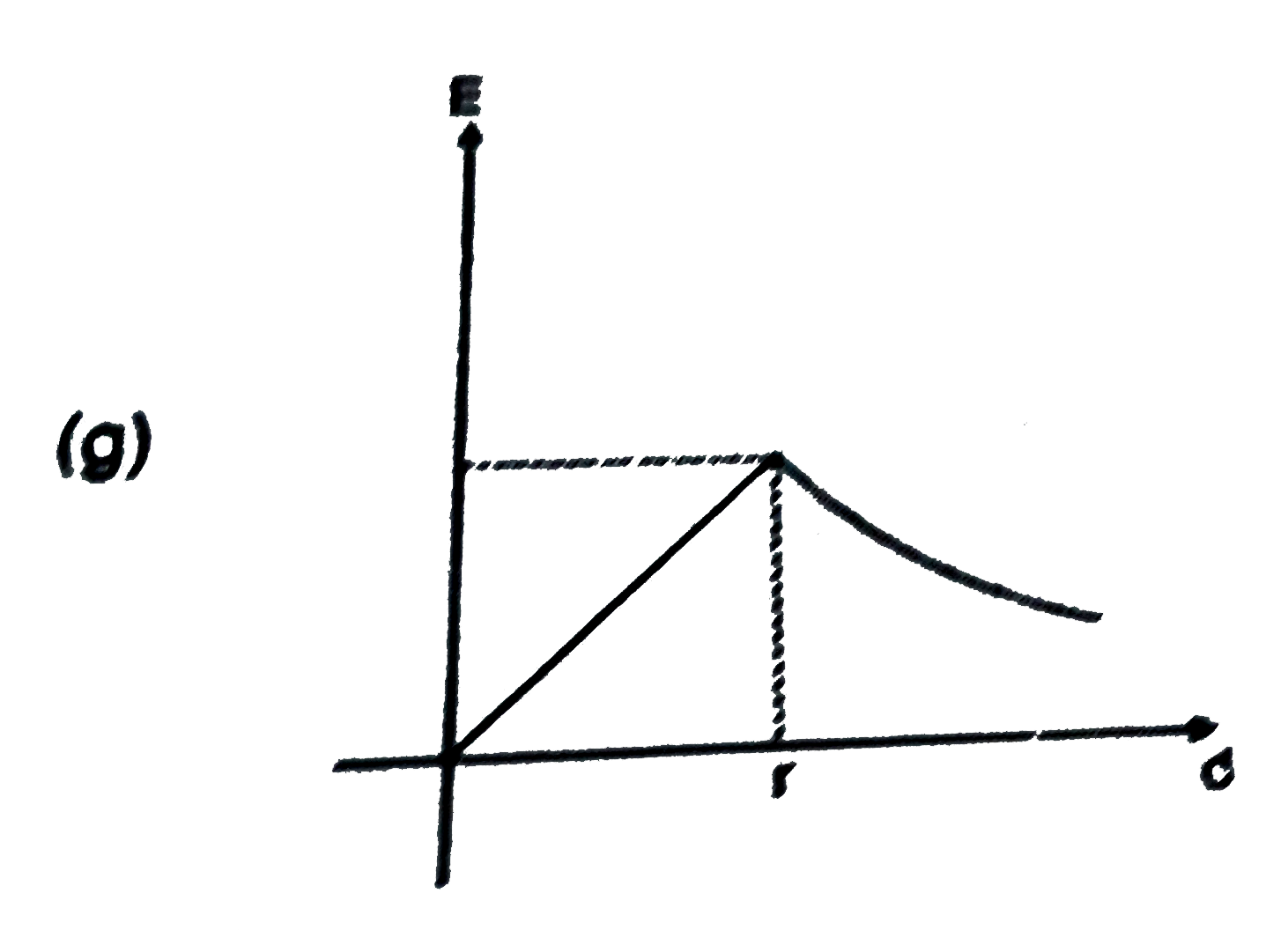
t=π2W
E=μ0Ni0ωd2ld<r
E=μ0Ni0ωr22dld≥r
Lines of force

Similar Questions
A long solenoid of length l=2.0 m , radius r=0.1 m and total number of turns N=1000 is carrying a current i0=20.0A. The axis of the solenoid coincides with the z-axis.
(a) State the expression for the magnetic field of the solenoid and calculate its value ? Magnetic field.
(b) Obtain the expression for the self - inductance (L) of the solenoid. Calculate its value. Value of L .
View SolutionA solenoid coil of 300turns/m is carrying a current of 5A. The length of the solenoid is 0⋅5m and has a radius of 1cm. Find the magnitude of the magnetic field well inside the solenoid.
View Solution
Knowledge Check
A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. The magnetic field inside the solenoid is
A3.14×10−3TB6.28×10−3TC9.14×10−3TD1.68×10−3TA solenoid of radius R and length L has a current I=I0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is
Aμ0nl0ωR22rsinωtBμ0nl0ωR2rsinωtCμ0nl0R2rsinωtDzeroThe expression for magnetic induction inside a solenoid of length L carrying a current I and having N number of turns is
Aμ04πNLIBμ0NICμ04πNLIDμ0NLI
A thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionA thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionA long solenoid of length 'l' having carries a current I. Deduce the expression for the magnetic field in the interior of the solenoid.
View SolutionThe expression for magnetic induction inside a solenoid of length L carrying a current I and having N number of turns is
View SolutionA long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View Solution
