If accleration due to gravity on the surface of earth is $10 m s^{- 2}$ and let acceleration due to gravitational acceleration at surface of another planet of our solar system be $5 m s^{- 2}$ An astronaut weighing $50 k g$ on earth goes to this planet in spaceship with a constant velcity The weight of the astronaut with time of fiight is roughly given by
.

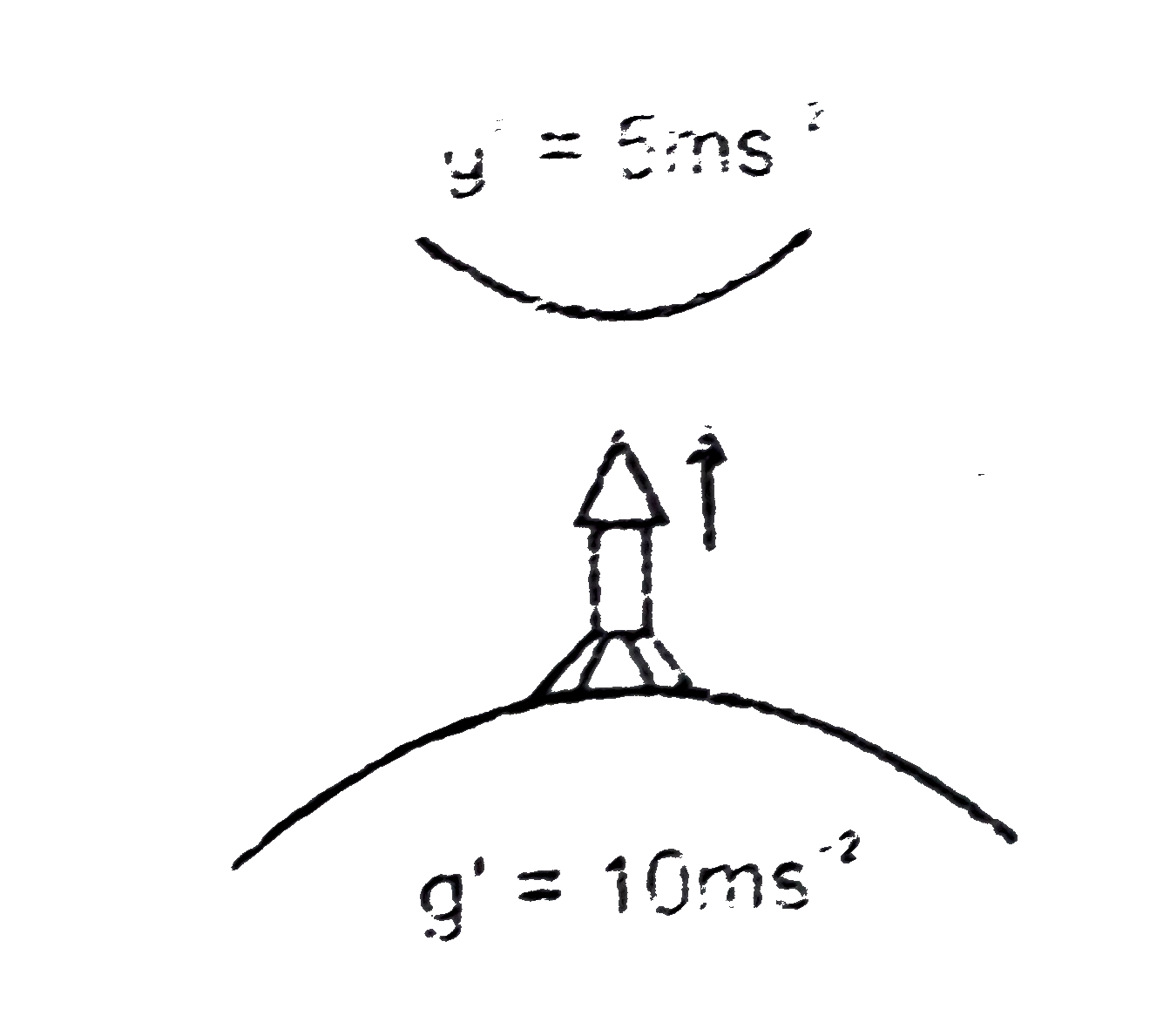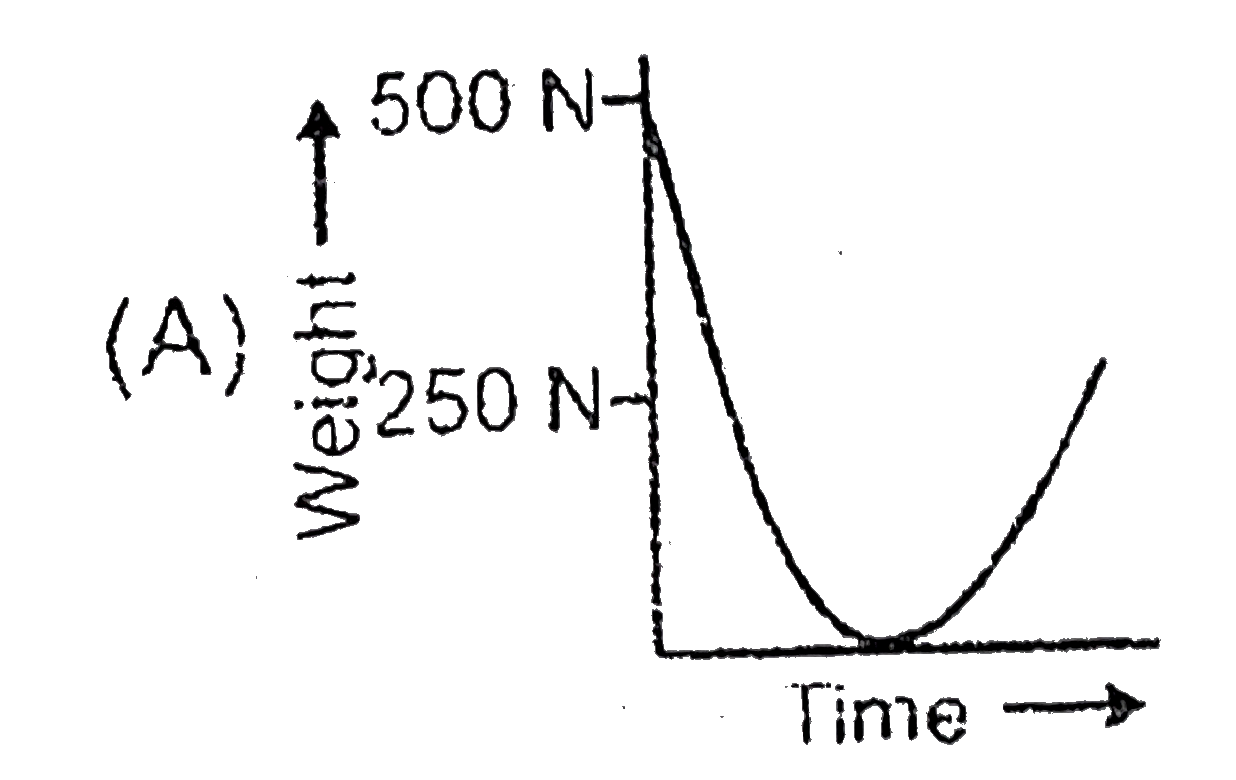
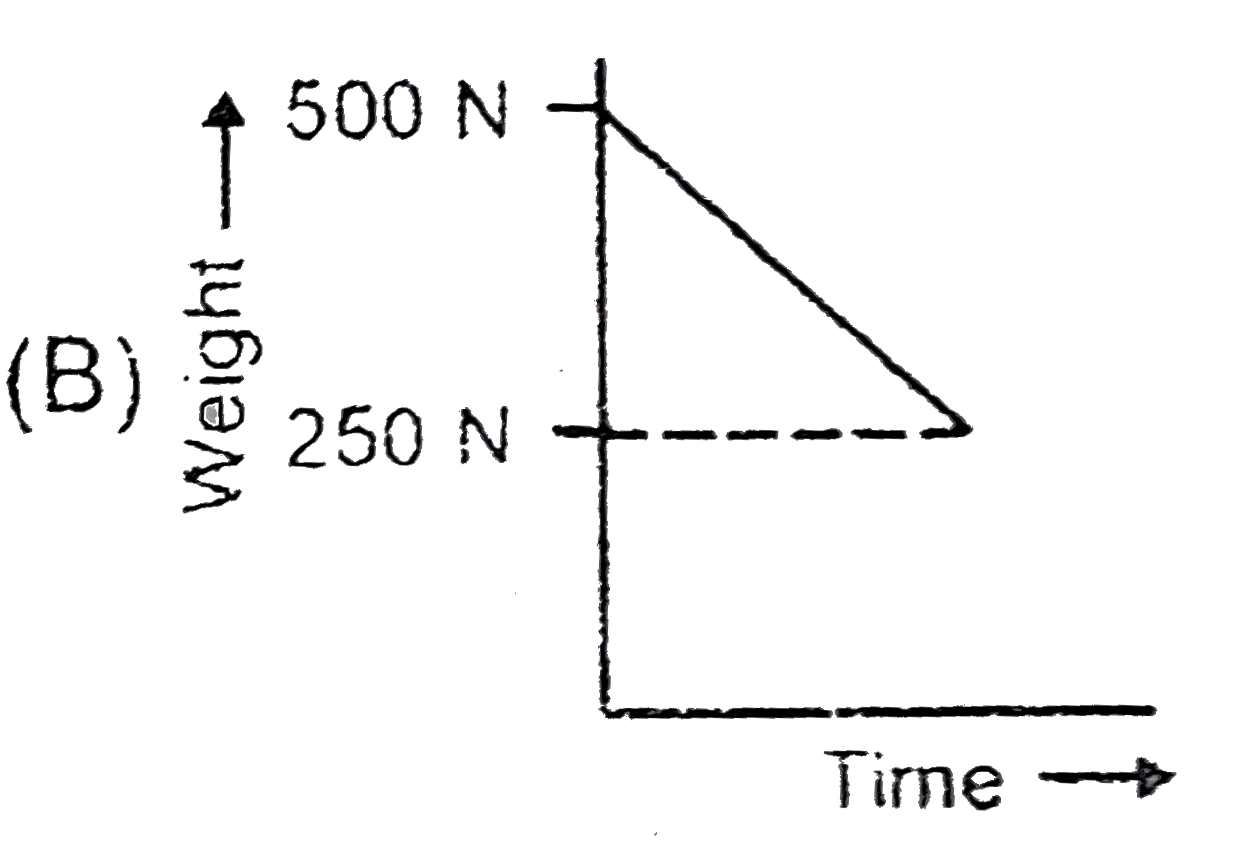
ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for If accleration due to gravity on the surface of earth is 10ms^(-2) and let acceleration due to gravitational acceleration at surface of another planet of our solar system be 5ms^(-2) An astronaut weighing 50kg on earth goes to this planet in spaceship with a constant velcity The weight of the astronaut with time of fiight is roughly given by . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Acceleration due to gravity at earth's surface is $10 m s^{- 2}$ . The value of acceleration due to gravity at the surface of a planet of mass ${(\frac{1}{5})}^{t h}$ and radius $\frac{1}{2}$ of the earth is
A $4 m s^{- 2}$
B $6 m s^{- 2}$
C $8 m s^{- 2}$
D $12 m s^{- 2}$
Question 2 - Select One
Acceleration due to gravity at earth's surface is $10 m^{- 2}$ The value of acceleration due to gravity at the surface of a planet of mass $\frac{1}{2}$ th and radius $\frac{1}{2}$ of f the earth is -
A $5 m s^{- 2}$
B $10 m s^{- 2}$
C $20 m s^{- 2}$
D $40 m s^{- 2}$
Question 3 - Select One
If the acceleration due to gravity on the surface of earth is g, then the acceleration due to gravity on the surface of a planet whose mass is same as that of earth and radius is half as that of earth is _________________.
A2g
Bg/4
Cg/2
D4g

RESONANCE-GRAVITATION-EXERCISE-1 PART-2

Home
Ask Doubt
Profile

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

Acceleration due to gravity at earth's surface is 10ms−2. The value of acceleration due to gravity at the surface of a planet of mass (15)th and radius 12 of the earth is

Acceleration due to gravity at earth's surface is 10m−2 The value of acceleration due to gravity at the surface of a planet of mass 12 th and radius 12 of f the earth is -

If the acceleration due to gravity on the surface of earth is g, then the acceleration due to gravity on the surface of a planet whose mass is same as that of earth and radius is half as that of earth is _________________.

RESONANCE-GRAVITATION-EXERCISE-1 PART-2

Acceleration due to gravity at earth's surface is $10 m s^{- 2}$ . The value of acceleration due to gravity at the surface of a planet of mass ${(\frac{1}{5})}^{t h}$ and radius $\frac{1}{2}$ of the earth is

Acceleration due to gravity at earth's surface is $10 m^{- 2}$ The value of acceleration due to gravity at the surface of a planet of mass $\frac{1}{2}$ th and radius $\frac{1}{2}$ of f the earth is -