vec(a)(1)+vec(a)(2) -vec(b)(1)-vec(b)(2)=0

Let $a_{1} & a_{2}$ are the acceleration of A & B. Let $b_{1} & b_{2}$ the acceleration of C & D relative to the wedges A and B respectively, choose the right relation. (directions of $a_{1}, a_{2}, b_{1} & b_{2}$ are shown in figure below) :

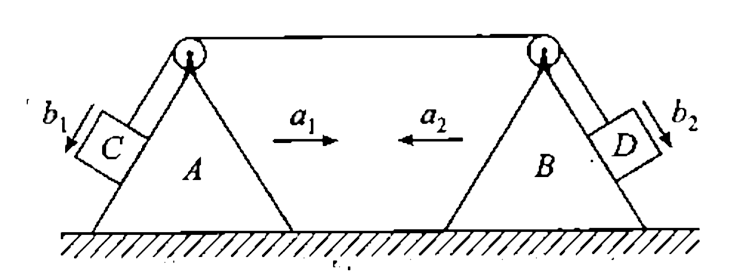A $a_{1} - a_{2} + b_{1} - b_{2} = 0$
B $a_{1} + a_{2} - b_{1} - b_{2} = 0$
C $a_{1} + a_{2} + b_{1} + b_{2} = 0$
D $a_{1} + b_{2} = a_{2} + b_{1}$
Let $\to C = \to A + \to B$ then
A $∣ ∣ \to C ∣ ∣$ is always greater then $∣ ∣ \to A ∣ ∣$
BIt is possible to have $∣ ∣ \to C ∣ ∣ < ∣ ∣ \to A ∣ ∣ and ∣ ∣ \to C < ∣ ∣ \to B ∣ ∣$
C $C$ is always equal to $A + B$
D $C$ is never equal to $A + B$
Let $\to C = \to A + \to B$ :
A $∣ ∣ \to C ∣ ∣$ is always greater than $∣ ∣ \to A ∣ ∣$
BIt is possible to have $∣ ∣ \to C ∣ ∣ < ∣ ∣ \to A ∣ ∣$ and $∣ ∣ \to C ∣ ∣ < ∣ ∣ \to B ∣ ∣$
C $∣ ∣ \to C ∣ ∣$ is always equal to $∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$
D $∣ ∣ \to C ∣ ∣$ is never equal to $∣ ∣ \to A ∣ ∣ + ∣ ∣ \to B ∣ ∣$

Let ${\to a}_{1}$ and ${\to a}_{2}$ are the acceleration of wedges A and B. Let ${\to b}_{1}$ and ${\to b}_{1}$ be the accelerations of C and D relative to wedges A and B respectively. Choose the right relation $:$