Draw the graph of the function y=3x4−4x3. Discuss the points of local extremum, inflection and intervals of monotonicity.
Video Solution
Text Solution
We have y=f(x)=3x4−4x3=x3(3x−4)
The sign scheme of y=f(x) is as follows.
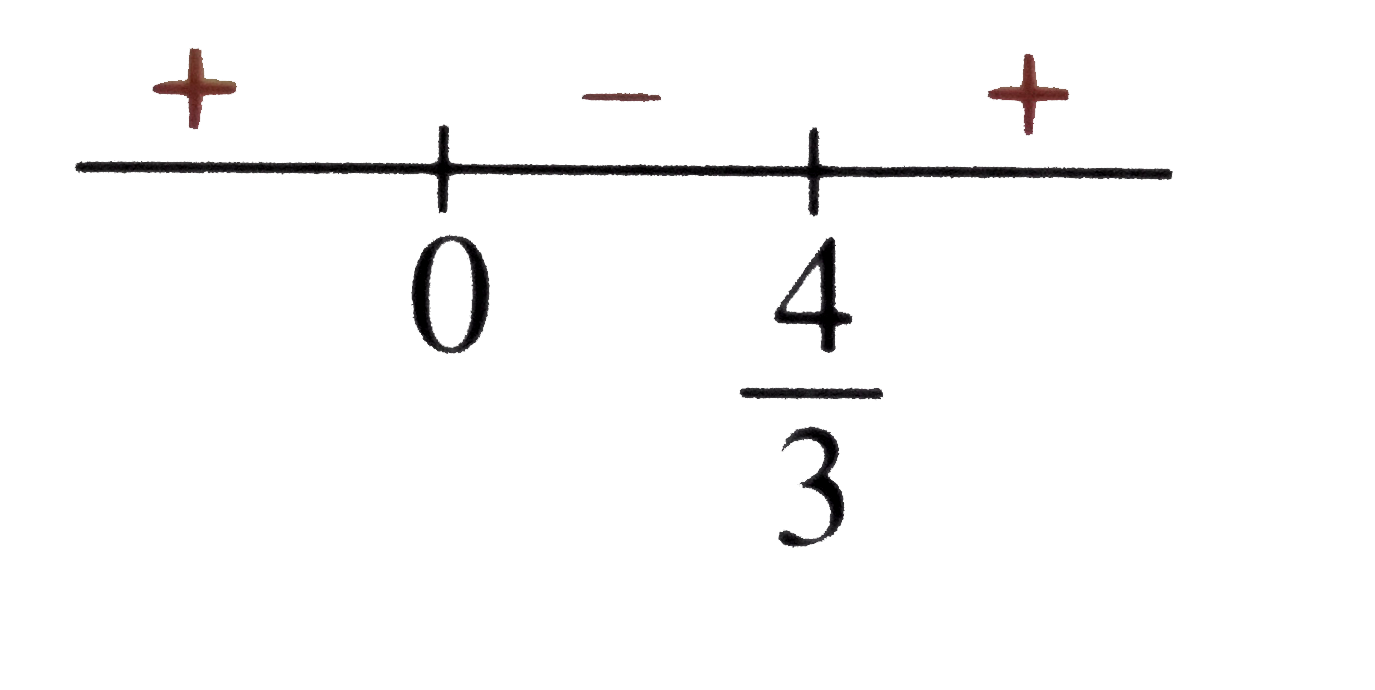
(3x−4)→ Graph crosses the x-axis at x=4/3 without touching the x-axis.
x2→ Graph crosses the x-axis at (0,0) and also touches the x-axis at this point.
f'(x)=12x3−12x2
=12x2(x−1)
f'(x)=0
∴ x=0,1
f'(x)<0,if x<1, where f(x) decreases
f'(x)>0,if x>1, where f(x) increases
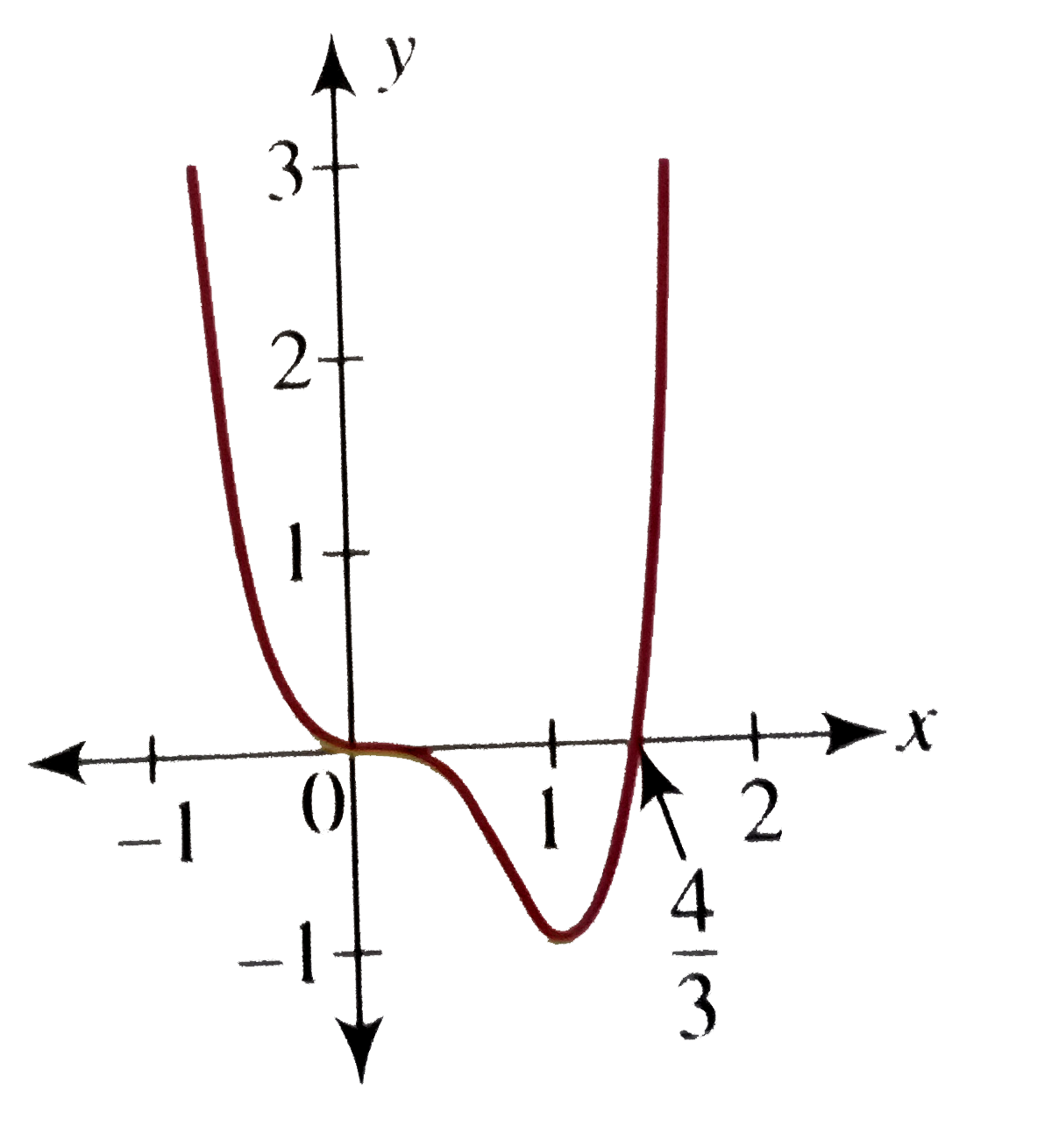
x=1 is the point of minima.
Also f''(x)=36x2−24x=12x(3x−2)
f''(x)=0,if x=0,2/3, which are points of inflection .
The graph of the function is as shown in the following figure.
|
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
Similar Questions
Draw the graph : x+y=4
View SolutionDraw the graph of the polynomial f(x)=x3−4x .
View SolutionDraw the graphs of following: y=x3−4x4
View SolutionDraw the graph of following function y=4x3−30x2+72x−55
View SolutionDraw a graph of the equation: 3x−2y=4 and x+y−3=0
View SolutionDraw and discuss the graph of the function f(x)=e1/x
View SolutionDraw the graph of the following function: h(x)=∣∣tan−1(3x)∣∣
View SolutionDraw the graph of the function y= 3x and from the graph , find the value of y, when
x=4
View SolutionDraw a graph of the function y=[x]+|1−x|,−1≤x≤3. Determine the points if any, where this function is not differentiable.
View SolutionDraw the graph of the function y= 3x and from the graph , find the value of y, when
x = 5
View Solution
