Draw the graph of $y = x^{3} - x^{2} + x - 2$ and find the number of real root(s) of the equation $x^{3} - x^{2} + x - 2 = 0$ . Also locate the root.

Video Solution

Text Solution

Verified by Experts

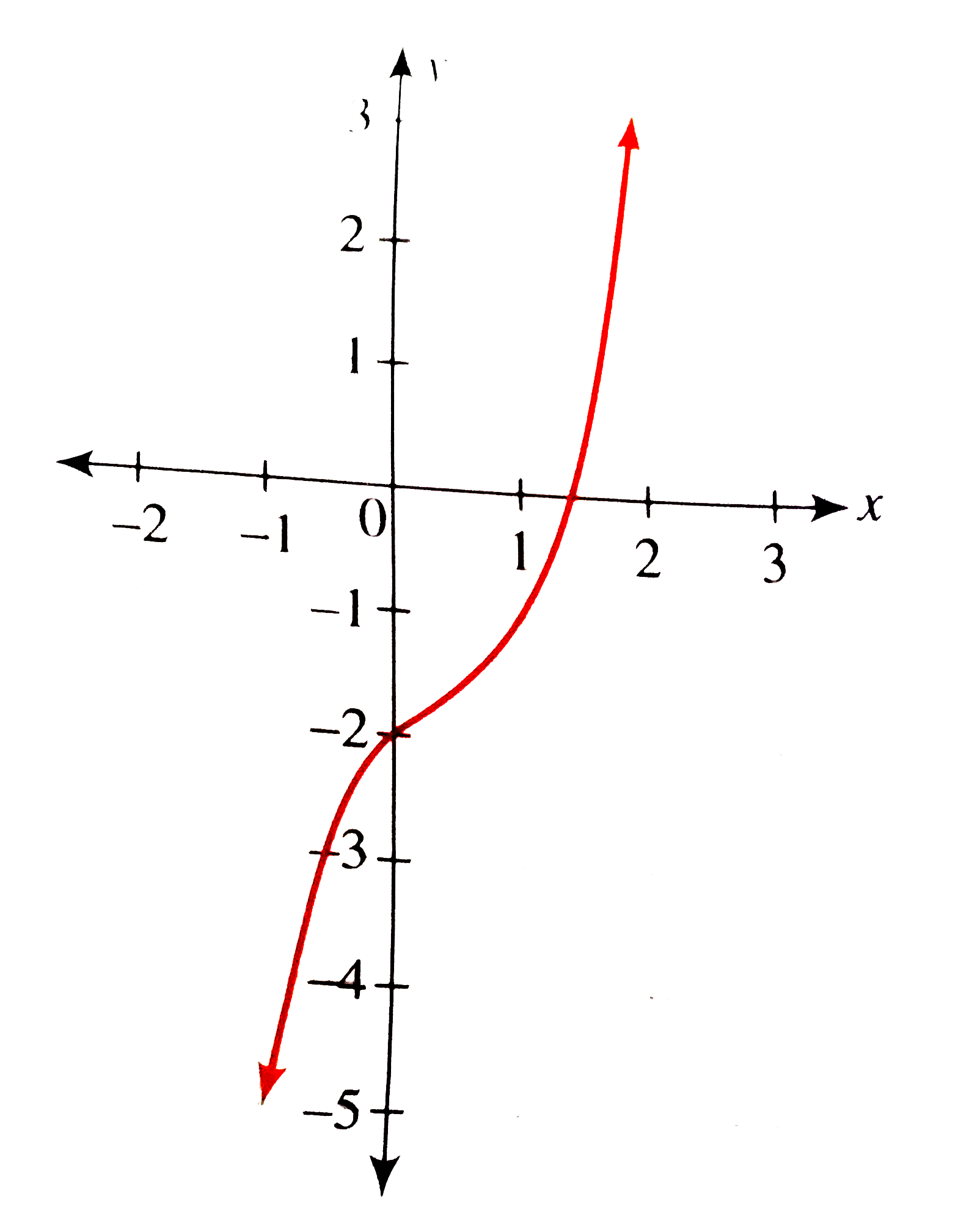
We have $y = f (x) = x^{3} - x^{2} + x - 2$
$\frac{d y}{d x} = 3 x^{2} - 2 x + 1 > 0, \forall x \in R$
So $y = f (x)$ increases.
Since the leading coefficient is '3', when $x \to \infty, f (x) \to \infty$ and when $x \to - \infty, f (x) \to - \infty$ .
$f (0) = - 2$ , hence the graph cuts the x-axis for some positive value of x.
Thus, the graph will cut the x-axis at one point only.
Also $f (1) = - 1$ and $f (2) = 4$ .
Thus, the graph will cut the x-axis somewhere between '1' and '2'.
From the above discussion, the graph of $y = f (x)$ can be drawn as shown in the following figure.

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The number of real roots of the equation ${| x |}^{2} - 3 | x | + 2 = 0$ , is
A $4$
B $3$
C $2$
D $1$
The number of real root of the equation $e^{x - 1} + x - 2 = 0$ , is
A1
B2
C3
D4
The number of real roots of the equation $2 x^{3} - 3 x^{2} + 6 x + 6 = 0$ is
A1
B2
C3
Dnone of these

CENGAGE-GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS-Exercise

Home
Ask Doubt
Profile