If f(x)=sgn(x) and g(x)=x3,then prove that limx→0f(x).g(x) exists though limx→0f(x) does not exist.
Video Solution
Text Solution
f(x)=sgn(x)=⎧⎪⎨⎪⎩1, x>0−1, x<00, x=0
∴ limx→0+f(x)=1 and limx→0+f(x)=−1
Now f(x)×g(x)=⎧⎪⎨⎪⎩x3, x>0−x3, x<00, x=0
∴ limx→0+f(x).g(x)=limx→0+x3=0
and limx→0−f(x).g(x)=limx→0+(−x3)=0
Thus limx→0f(x).g(x) exists.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.315videos
LIMITS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.45videos
LIMITS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.110videos
LIMITS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
- BOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.210videos
LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
limx→0sin|x|x equal to ?
A1B−1C∞DLimit D.N.E. - Question 2 - Select One
What is limx→0ax−bxx?
Alog(ab)Blog(ba)CabDlog (ab) - Question 3 - Select One
What is limx→0ex−(1+x)x2 equal to ?
Alog(ab)BlogbaCabDlog (Ab)
If f(x)=|x−1|x−1 prove that limx→1f(x) does not exist.
View SolutionSlove limx→0(1+x)1/x−ex
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?
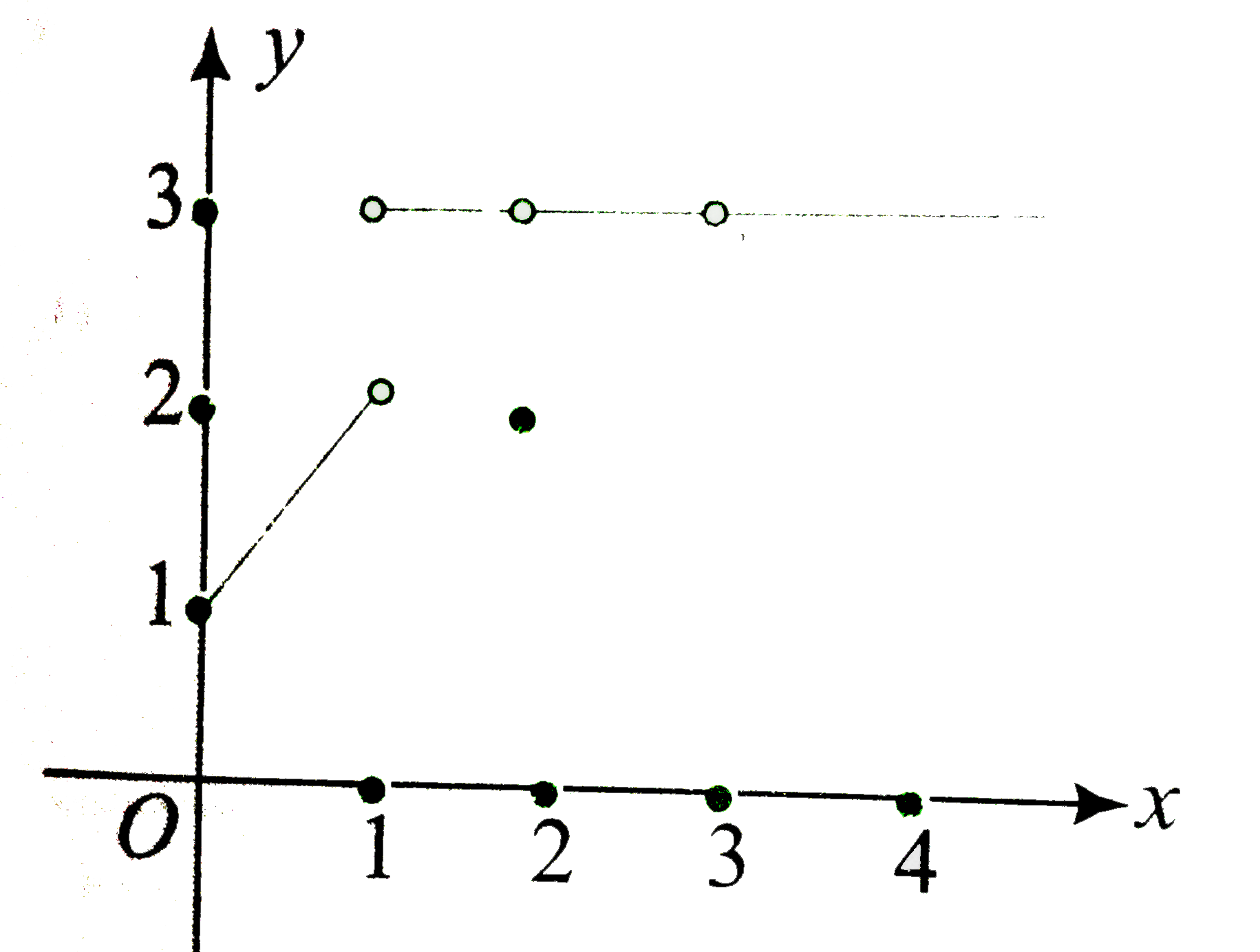
(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.View SolutionIf f is an even function, prove that limx→0−(x)=limx→0+f(x).
View Solutionlimx→0ax−bxx equal to ?
View Solution

