limx→0[(1−ex)sinx|x|] is (where [.] represents the greatest integer function )
1
2
3
none of these
The correct Answer is:A
To solve the limit limx→0(1−ex)sinx|x| and find the greatest integer function of the result, we will evaluate the left-hand limit and the right-hand limit separately.
Step 1: Define the limit
We need to evaluate the limit as x approaches 0. We will consider two cases: when x approaches 0 from the left (negative) and from the right (positive).
Step 2: Evaluate the left-hand limit
For x<0:
- The modulus function |x|=−x.
- Thus, we rewrite the limit:
limx→0−(1−ex)sinx|x|=limx→0−(1−ex)sinx−x
Step 3: Simplify the left-hand limit
Now, we can evaluate the limit:
limx→0−(1−ex)sinx−x=−limx→0−(1−ex)sinxx
Using the fact that sinx≈x as x→0, we can substitute:
limx→0−(1−ex)sinxx=limx→0−(1−ex)⋅sinxx
As x→0, sinxx→1.
Step 4: Evaluate 1−ex
As x→0−, ex→1, so:
1−ex→1−1=0
Thus, we have:
limx→0−(1−ex)⋅1=0
Step 5: Evaluate the right-hand limit
For x>0:
- The modulus function |x|=x.
- Thus, we rewrite the limit:
limx→0+(1−ex)sinx|x|=limx→0+(1−ex)sinxx
Step 6: Simplify the right-hand limit
Using the same reasoning as before:
limx→0+(1−ex)sinxx=(1−e0)⋅1=0
Step 7: Combine the results
Both the left-hand limit and the right-hand limit are equal to 0:
limx→0−(1−ex)sinx|x|=0
limx→0+(1−ex)sinx|x|=0
Step 8: Final limit
Thus, we conclude:
limx→0(1−ex)sinx|x|=0
Step 9: Apply the greatest integer function
Now we apply the greatest integer function:
⌊0⌋=0
Final Answer
The final answer is:
0
We need to evaluate the limit as x approaches 0. We will consider two cases: when x approaches 0 from the left (negative) and from the right (positive).
For x<0:
- The modulus function |x|=−x.
- Thus, we rewrite the limit:
limx→0−(1−ex)sinx|x|=limx→0−(1−ex)sinx−x
Now, we can evaluate the limit:
limx→0−(1−ex)sinx−x=−limx→0−(1−ex)sinxx
Using the fact that sinx≈x as x→0, we can substitute:
limx→0−(1−ex)sinxx=limx→0−(1−ex)⋅sinxx
As x→0, sinxx→1.
As x→0−, ex→1, so:
1−ex→1−1=0
Thus, we have:
limx→0−(1−ex)⋅1=0
For x>0:
- The modulus function |x|=x.
- Thus, we rewrite the limit:
limx→0+(1−ex)sinx|x|=limx→0+(1−ex)sinxx
Using the same reasoning as before:
limx→0+(1−ex)sinxx=(1−e0)⋅1=0
Both the left-hand limit and the right-hand limit are equal to 0:
limx→0−(1−ex)sinx|x|=0
limx→0+(1−ex)sinx|x|=0
Thus, we conclude:
limx→0(1−ex)sinx|x|=0
Now we apply the greatest integer function:
⌊0⌋=0
The final answer is:
0
Topper's Solved these Questions
- LIMITSBook:CENGAGEChapter:LIMITSExercise:Exercise (Multiple)
Explore 18 Videos
- LIMITSBook:CENGAGEChapter:LIMITSExercise:Exercise (Comprehension)
Explore 20 Videos
- LIMITSBook:CENGAGEChapter:LIMITSExercise:Exercise 2.8
Explore 8 Videos
- JEE 2019Book:CENGAGEChapter:JEE 2019Exercise:Chapter 10
Explore 9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBook:CENGAGEChapter:LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSExercise:DPP 1.2
Explore 10 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
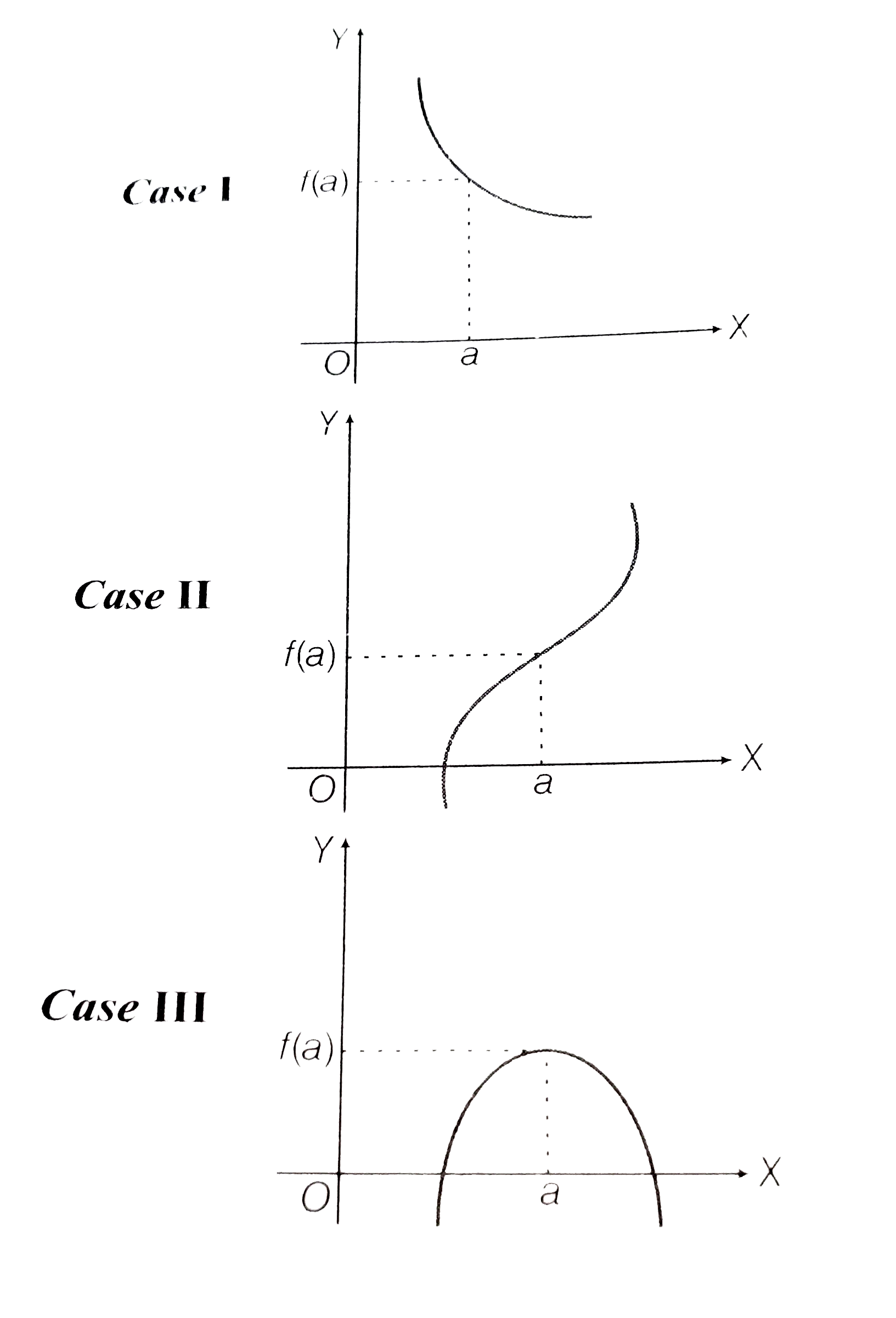
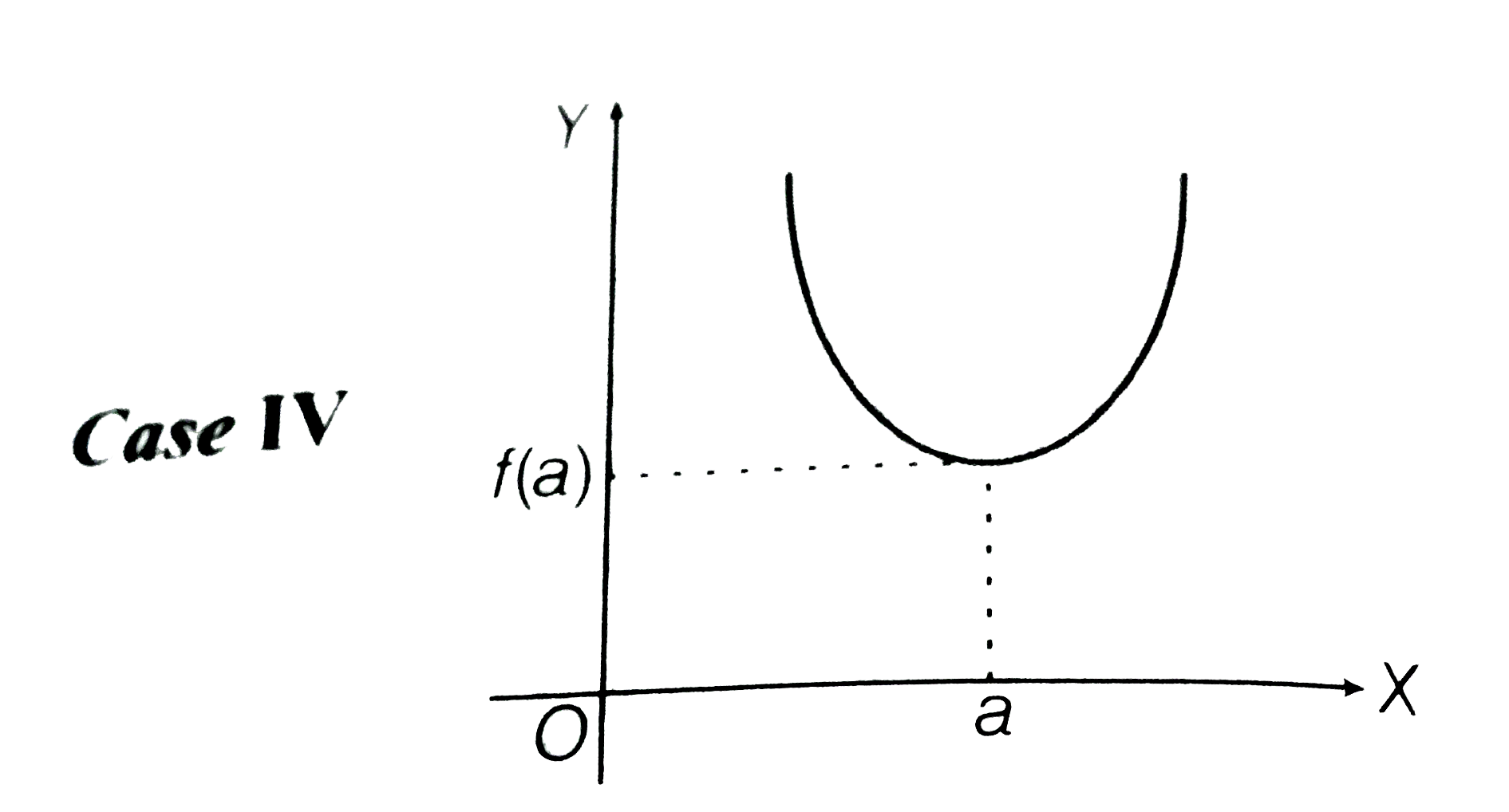
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.limx→0[(1−ex).sinx|x|] (where [.] denotes the greatest integer function) equals
View Solutionlimx→0[(1−ex)sinx|x|]is(where[.] represents the greatest integer function). (a)−1 (b) 1 (c) 0 (d) does not exist
View Solution
Knowledge Check
The value of limx→0sinx3[5x] is equal to
[where [.] represent the greatest integer function)A13B0C53D1limx→0[100tanxsinxx2] is (where [.] represents greatest integer function).
A99B100C0Dnon-existentlimx→0[(1−ex)sinx|x|] is equal to
( where [∗]denotes greatest integer function )A−1B1C0Ddoes not exist
Prove that [limx→0sinxx]=0, where [.] represents the greatest integer function.
View SolutionFind limx→0[x](e1/x−1e1/x+1), (where [.] represents the greatest integer funciton).
View SolutionEvaluate : [limx→0sinxx], where [⋅] represents the greatest integer function.
View SolutionEvalute [limx→0sin−1xx]=1, where[⋅] represets the greatest interger function.
View Solutionlimx→1[cosecπx2]1/(1−x) (where [.] represents the greatest integer function) is equal to
View Solution
