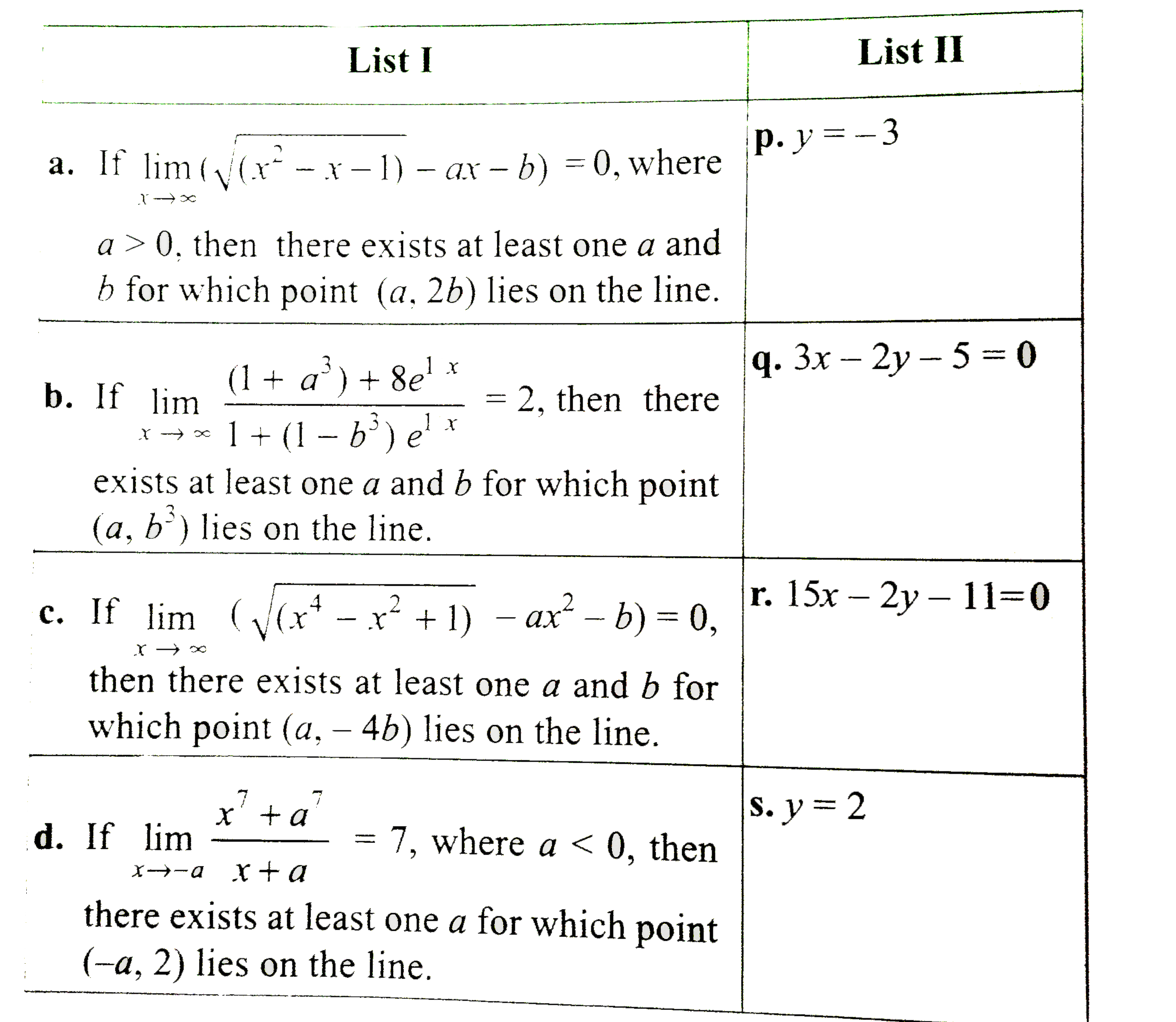
Match the following lists:

Text Solution

Verified by Experts

The correct Answer is: $a \to q; b \to p, q, r; c \to r, s; d \to r, s .$

a. Hence, $a > 0$ . Therfore.
$lim x \to \infty \frac{(\sqrt{(x^{2} - x + 1)} - a x - b) (\sqrt{x^{2} - x + 1)} + a x + b)}{(\sqrt{(x^{2} - x + 1)} + a x + b)}$
$= 0$
or $lim x \to \infty \frac{(x^{2} - x + 1) - {(a x + b)}^{2}}{\sqrt{(x^{2} - x + 1)} + a x + b} = 0$
or $lim x \to \infty \frac{(1 - a^{2}) x^{2} - (1 + 2 a b) x + (1 - b^{2})}{\sqrt{(x^{2} - x + 1)} + a x + b} = 0$
or $lim x \to \infty \frac{(1 - a^{2}) x - (1 + 2 a b) + \frac{(1 - b^{2})}{x}}{\sqrt{1 - \frac{1}{x} + \frac{1}{x^{2}} + a + \frac{b}{x}}} = 0$
This is possible only when
$1 - a^{2} = 0 and 1 + 2 a b = 0$
$∴ a = \pm 1$
or $a = 1 (∵ a > 0) (1)$
$∴ b = - 1 / 2$
$∴ (a, 2 b) \equiv (1, - 1)$
b. Divide numerator and denominator by $e^{1 / x}$ . Then,
$lim x \to \infty \frac{(1 + a^{3}) e^{- \frac{1}{x}} + 8}{e^{- \frac{1}{x}} + (1 - b^{3})} = 2$
or $\frac{0 + 8}{0 + 1 - b^{3}} = 2$
or $1 - b^{3} = 4$
$∴ b^{3} = - 3 or b = - 3^{1 / 3}$
Then, $a \in R .$ Therefore,
$(a, b^{3}) \equiv (a, - 3)$
c. $lim x \to \infty (\sqrt{(x^{4} - x^{2} + 1}) - a x^{2} - b) = 0$
Put $s = \frac{1}{t}$ .Then
$lim t \to 0 (\sqrt{(\frac{1}{t^{4}} - \frac{1}{t^{2}} + 1)} - \frac{a}{t^{2}} - b) = 0$
or $lim t \to 0 \frac{\sqrt{(1 - t^{2} + t^{4})} - a - b t^{2}}{t^{2}} = 0 (1)$
Since R.H.S. is finite, numerator must be equal to 0 at $t \to 0 .$
Therefore, $1 - a = 0 or a = 1 .$
From equation (1),
$lim t \to 0 \frac{\sqrt{(1 - t^{2} + t^{4})} - 1 - b t^{2}}{t^{2}} = 0$
$lim t \to 0 (- 1 + t^{2}) ⎛ ⎜ ⎝ \frac{{(1 - t^{2} + t^{4})}^{1 / 2} - {(1)}^{1 / 2}}{(1 - t^{2} + t^{4}) - 1} ⎞ ⎟ ⎠ = b$
or $(- 1) (\frac{1}{2}) = b or a = 1, b = - \frac{1}{2} or (a, - 4 b) \equiv (1, 2)$
d. $lim x \to - a \frac{x^{7} - {(- a)}^{7}}{x - (- a)} = 7 or 7 a^{6} = 7 or a^{6} = 1 or a = - 1$

|

Updated on:21/07/2023

Class 12 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

CENGAGE-LIMITS-Exercise (Matrix)

Home
Ask Doubt
Profile