Doubtnut Promotions Sticky

In a triangle ABC, side AB has equation 2x+3y=29 and side AC has equation x+2y=16. If the midpoint of BC is 5, 6), then find the equation of BC.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

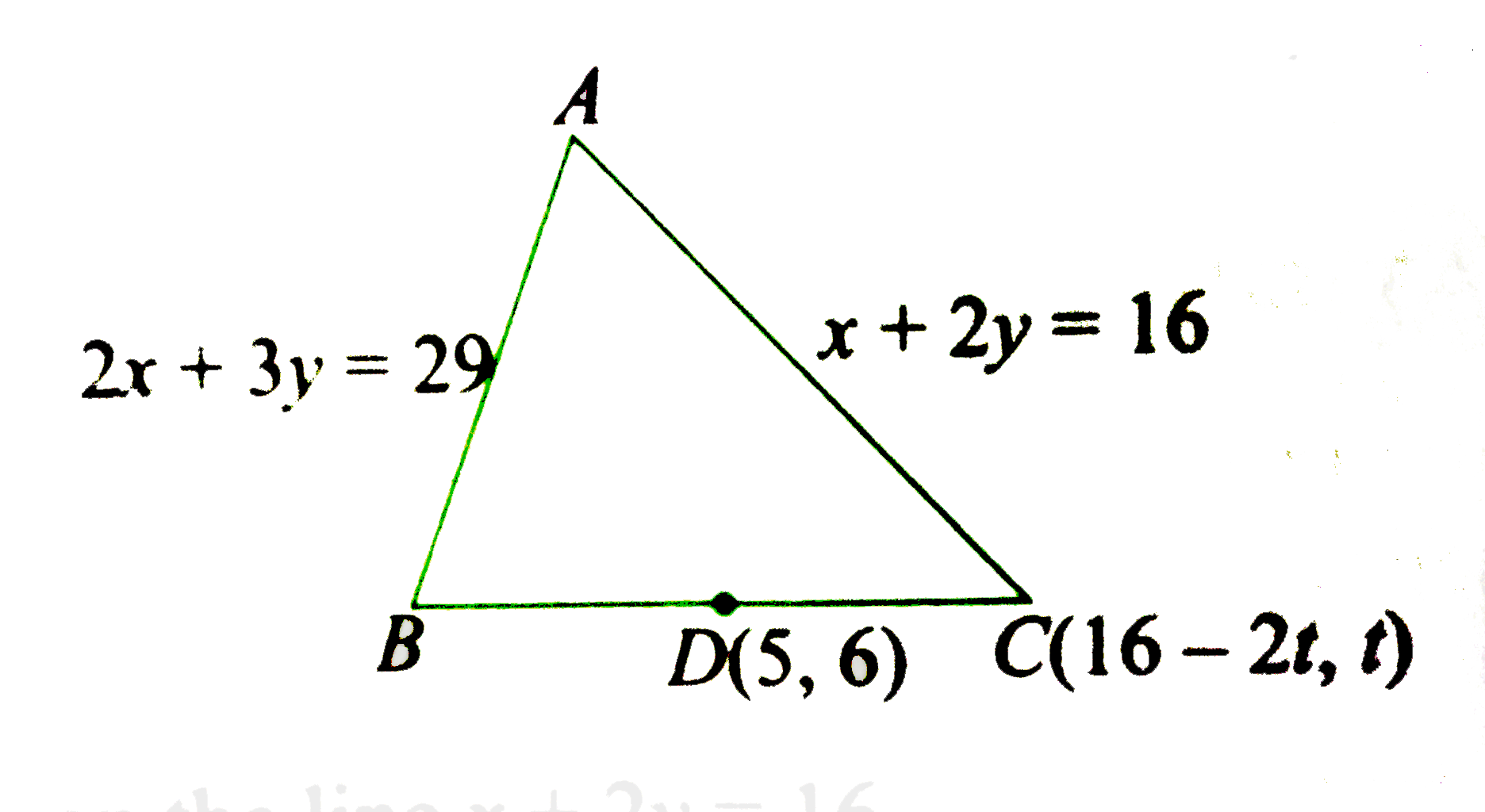
ocr_image
Vertex C lies on the line x+2y = 16.
So, let point C be (16-2t,t).
D(5,6) is midpoint of BC.
So, point B is (2t-6, 12-t)
Point B lies on the line 2x+3y-29 = 0
∴2(2t−6)+3(12−t)−29=0
⇒t=5
Hence, point B is (4,7)
Therefore, equation of line BC is
y−7=6−75−4(x−4)
or x+y = 11

|
Updated on:21/07/2023
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    In the equilateral triangle ABC, the equation of the side BC is x+y−2=0 and the centroid of ΔABC is (0, 0). If the points A, B, C are in anticlockwise oder, then the midpoint of the line segment joining A and C is

    A(−√3+12,√3+12)
    B(−√3−12,√3−12)
    C(−√3−12,√3+12)
    D(−√3+12,√3−12)
  • Question 2 - Select One

    In an equilateral triangle ABC, equation of the sides BC is x+y−2=0 and the centroid of ΔABC is (0, 0). If points A, B and C are in anticlockwise order, then the equation of side AC is

    A(y+2)=(2−√3)(x+2)
    B(y+2)=(2+√3)(x+2)
    C(y+1)=(2+√3)(x+1)
    Dx+2=0
  • Question 3 - Select One

    In a triangle ABC , if the equation of sides AB,BC and CA are 2x−y+4=0,x−2y−1=0andx+3y−3=0 respectively ,
    The equation of external bisector of angle B is

    Ax−y−1=0
    Bx−y+1=0
    Cx+y−5=0
    Dx+y+5=0