Sketch the origin in which the points satisfying the following inequality lie.
$(i) 2 x - 3 y - 5 > 0 (ii) - 3 x + 4 y + 7 > 0$
$(i i i) x > 2 (iv) y > - 3$

Video Solution

Text Solution

Verified by Experts

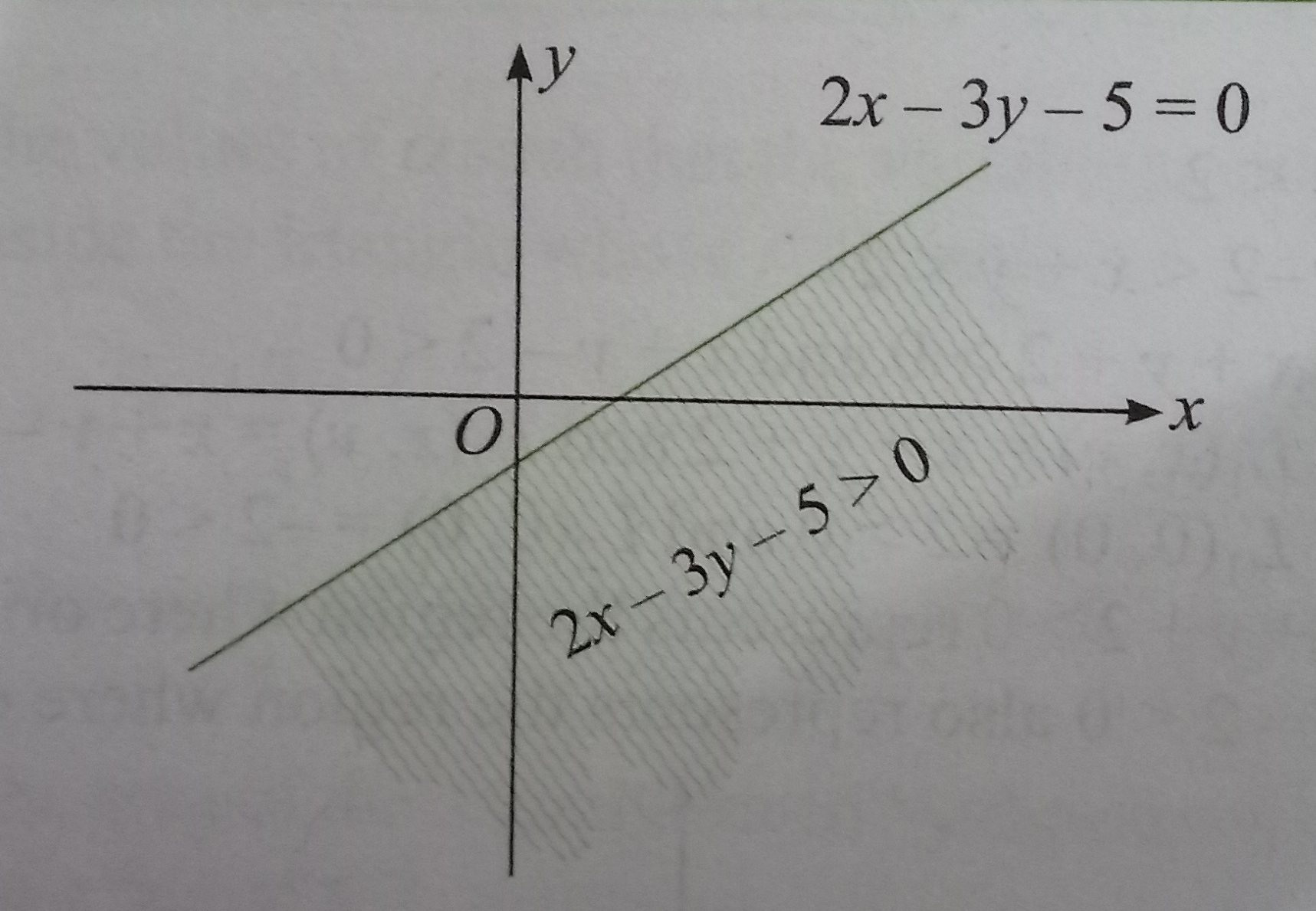
$(i) 2 x - 3 y - 5 > 0$
$Let L (x, y) = 2 x - 3 y - 5$
$L (0, 0) = - 5 < 0$
$So, 2 x - 3 y - 5 > 0$ represents the half origin of the plane where origin does not lie, i.e., below line 2x-3y-5=0.

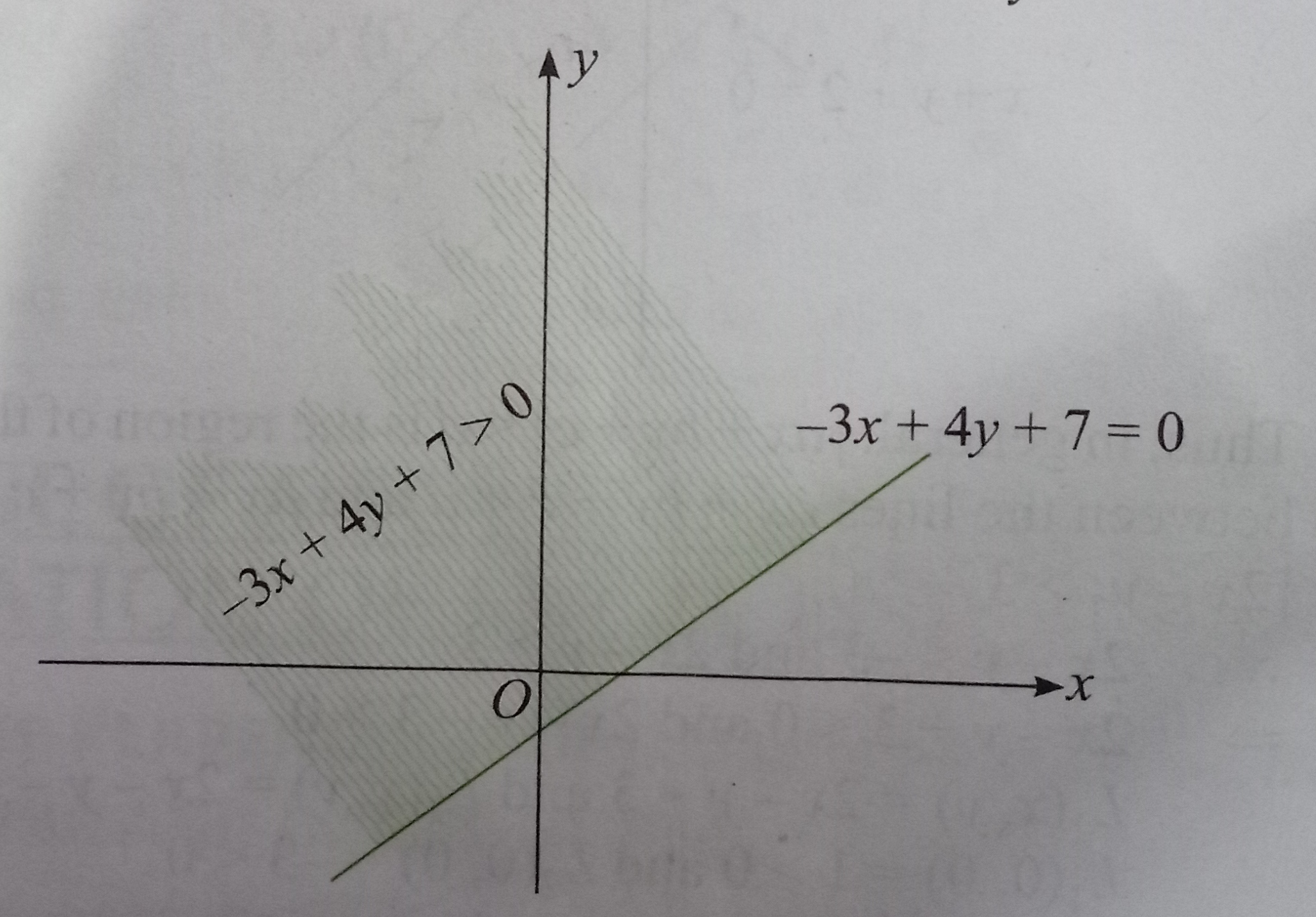
$(i i) - 3 x + 4 y + 7 > 0$
Let L(x,y) = -3x+4y+7
$L (0, 0) = 7 > 0$
$SO, - 3 x + 4 y + 7 > 0$ represents the half region of the plane where origin lies, i.e., above line -3x+4y+7=0.

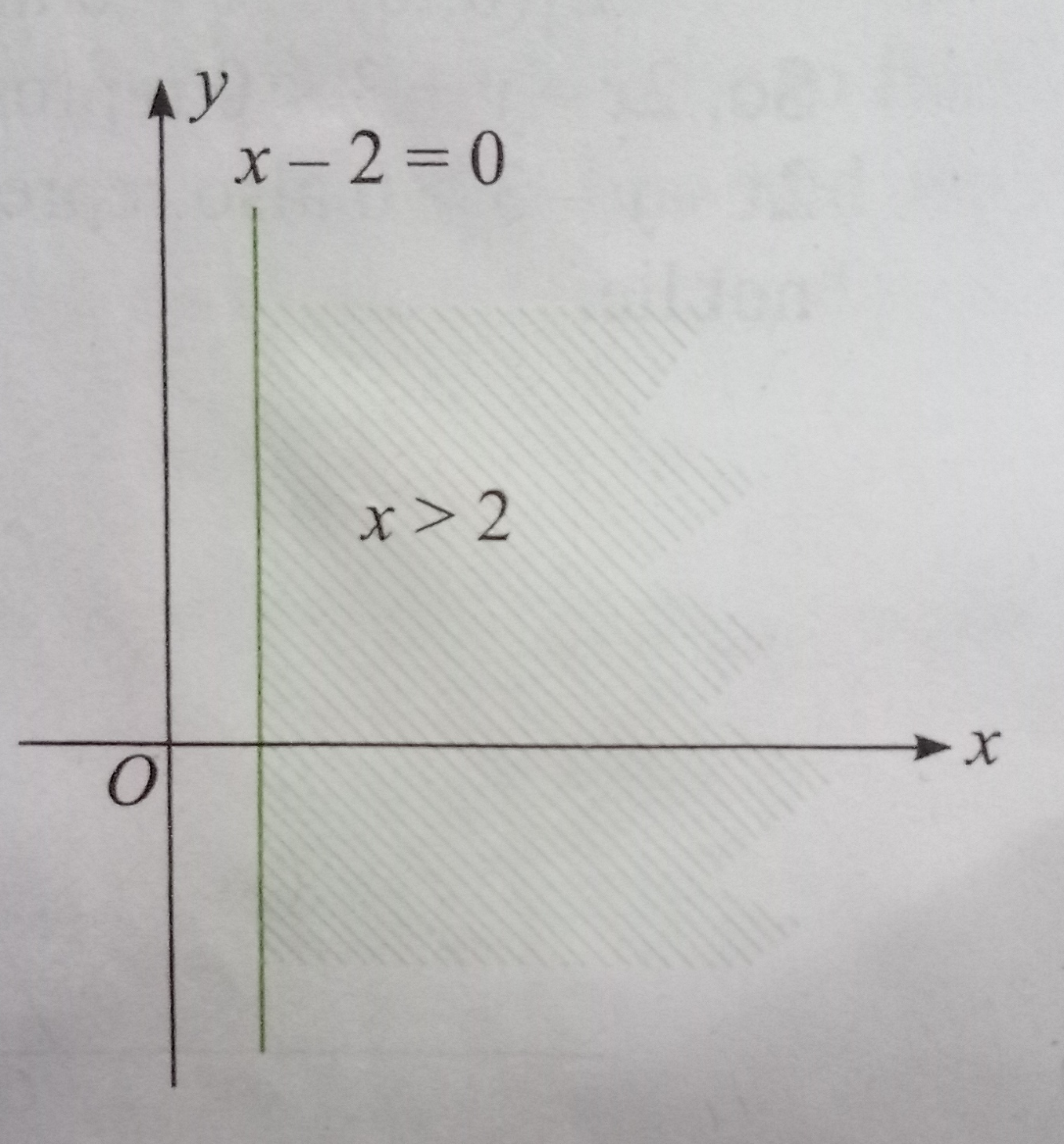
$(i i i) x > 2 or x - 2 > 0$
Let L(x,y) = x-2
$L (0, 0) = 0 - 2 < 0$
$So, x - 2 > 0$ represents the half region of the plane where origin does not lie, i.e., the right of the line x=2.
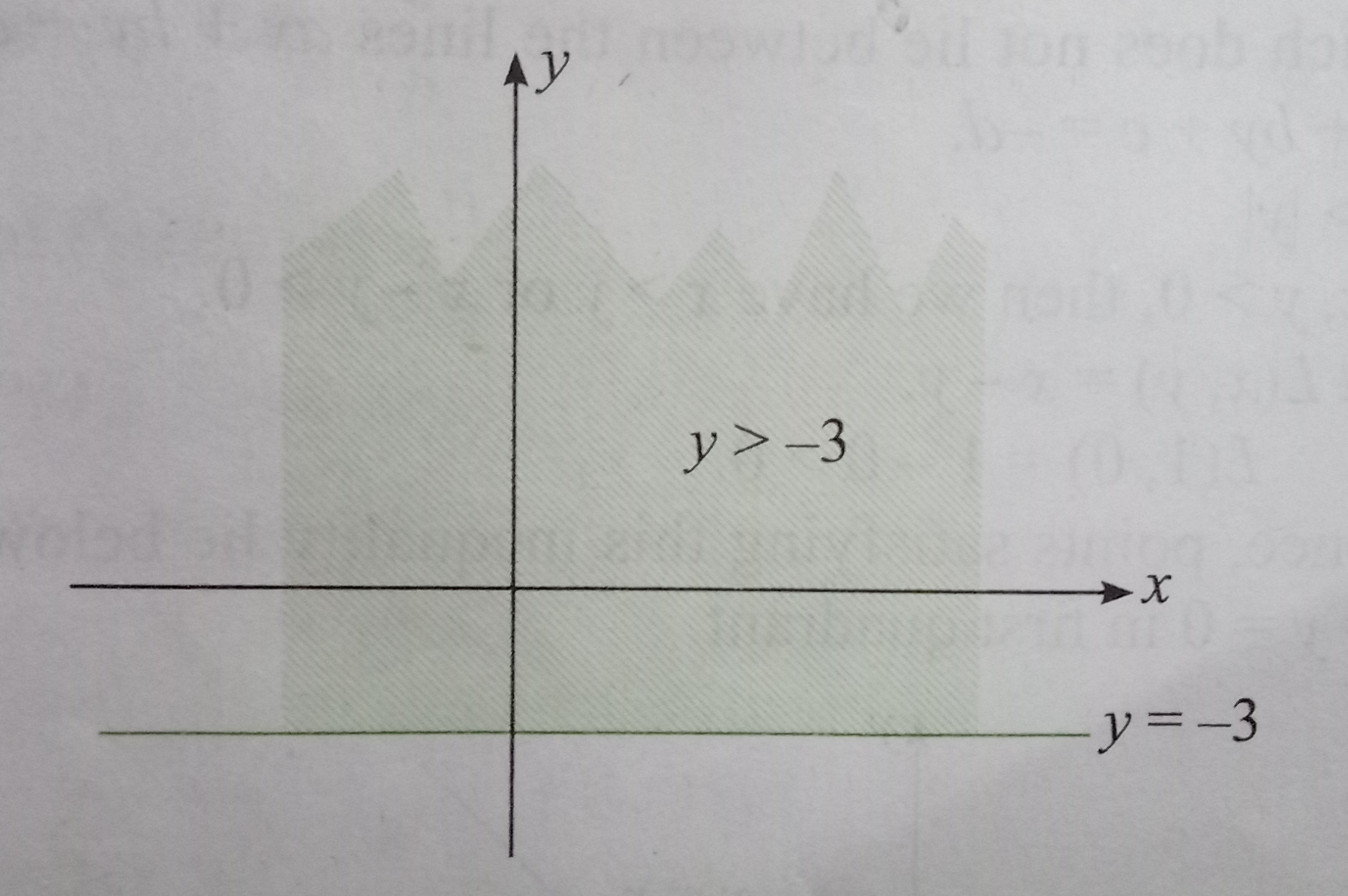
$(i v) y > - 3 or y + 3 > 0$
Let L(x,y) = y+3
$L (0, 0) = 0 + 3 > 0$
$S o, y + 3 > 0$ represents the half region of the plane where origin lies, i.e., above the line y+3=0.

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The solution set of the inequation $2 x + y > 5$ is
Ahalf plane that contains the origin
Bopen half plane not containing the origin
Cwhole xy-plane except the points typing on the line 2x + y = 5
DNone of these

CENGAGE-STRAIGHT LINES-JEE Advanced Previous Year

Home
Ask Doubt
Profile