Show that the lines $4 x + y - 9 = 0, x - 2 y + 3 = 0, 5 x - y - 6 = 0$ make equal intercepts on any line of slope 2.

Video Solution

Text Solution

Verified by Experts

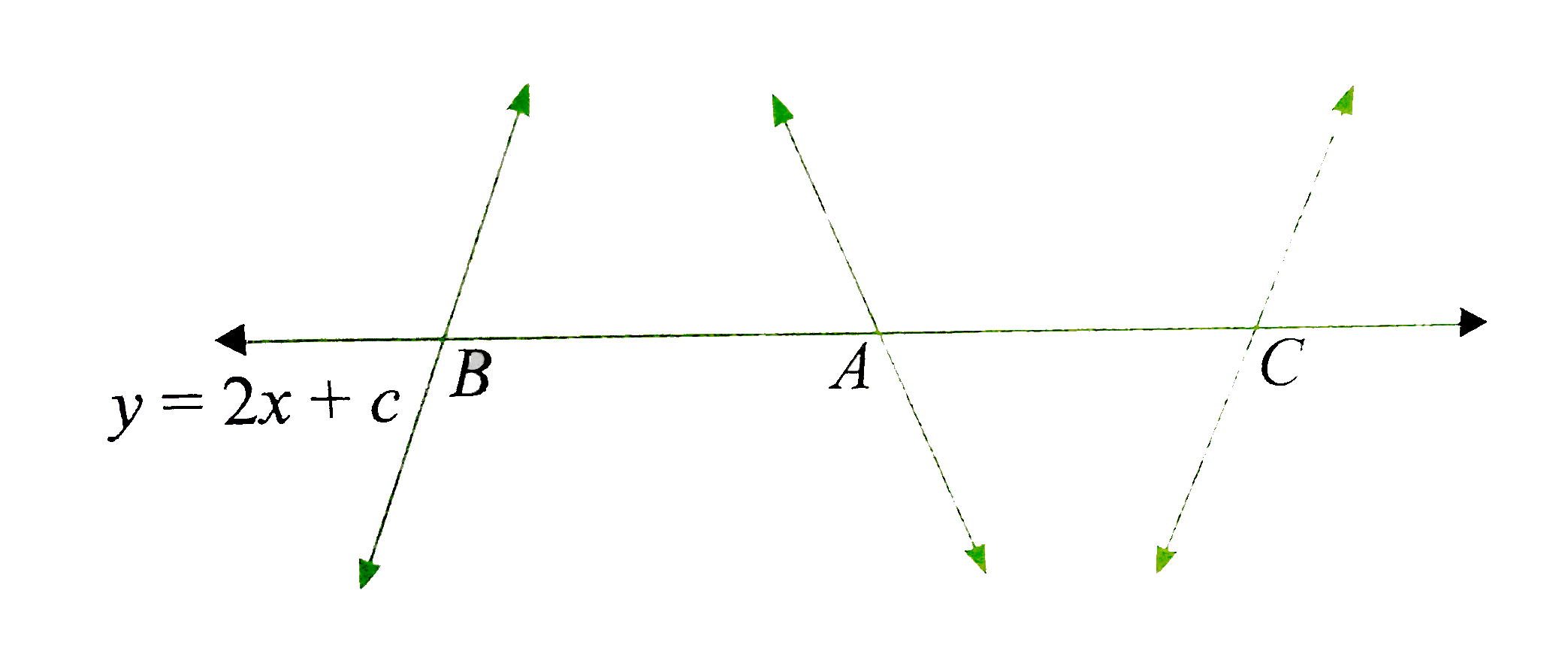
The given lines are
$4 x + y - 9 = 0 (1)$
$x - 2 y + 3 = 0 (2)$
$5 x - y - 6 = 0 (3)$
Now, the equation of any line having slope (gradient) 2 will be
$y = 2 x + c (4)$
Let line (4) cuts line (1), (2), and (3) at A,B, and C. respectively.
Solving (1) and (4), we get
$A \equiv (\frac{3}{2} - \frac{c}{6}, 3 + \frac{2 c}{3})$
$Similary, B \equiv (1 - \frac{2 c}{c}, 2 - \frac{c}{3})$
$and C \equiv (2 + \frac{c}{3}, 4 + \frac{5 c}{3})$
Clearly , A is the middle point of BC, Hene, AB=AC.

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The lines $x + 2 y - 5 = 0, 2 x - 3 y + 4 = 0, 6 x + 4 y - 13 = 0$
Aare concurrent
Bform a right angled triangle
Cform an isosceles triangle
Dform an equilateral triangle.
Question 2 - Select One
Let the lines $4 x - 3 y + 10 = 0$ and $4 x - 3 y - 30 = 0$ make equal intercepts of 6 units with a circle (C ) whose centre lies on $2 x + y = 0$ , then the equation of the circle C is
A $x^{2} + y^{2} - 2 x + 4 y - 20 = 0$
B $x^{2} + y^{2} - 4 x + 8 y - 20 = 0$
C $x^{2} + y^{2} + 2 x - 4 y - 20 = 0$
D $x^{2} + y^{2} - 4 x + 8 y - 5 = 0$
Question 3 - Select One
A line passes through the point of intersection of the lines 3x+y+1=0 and 2x-y+3=0 and makes equal intercepts with axes. Then, equation of the line is
A5x+5y-3=0
Bx+5y-3=0
C5x-y-3=0
D5x+5y+3=0

CENGAGE-STRAIGHT LINES-JEE Advanced Previous Year

Home
Ask Doubt
Profile