Question

A regular polygon has two of its consecutive diagonals as the lines $\sqrt{3}x+y-\sqrt{3}$
and $2y=\sqrt{3}$
. Point $(1,c)$
is one of its vertices. Find the equation of the sides of the polygon
and also find the coordinates of the vertices.

Explanation

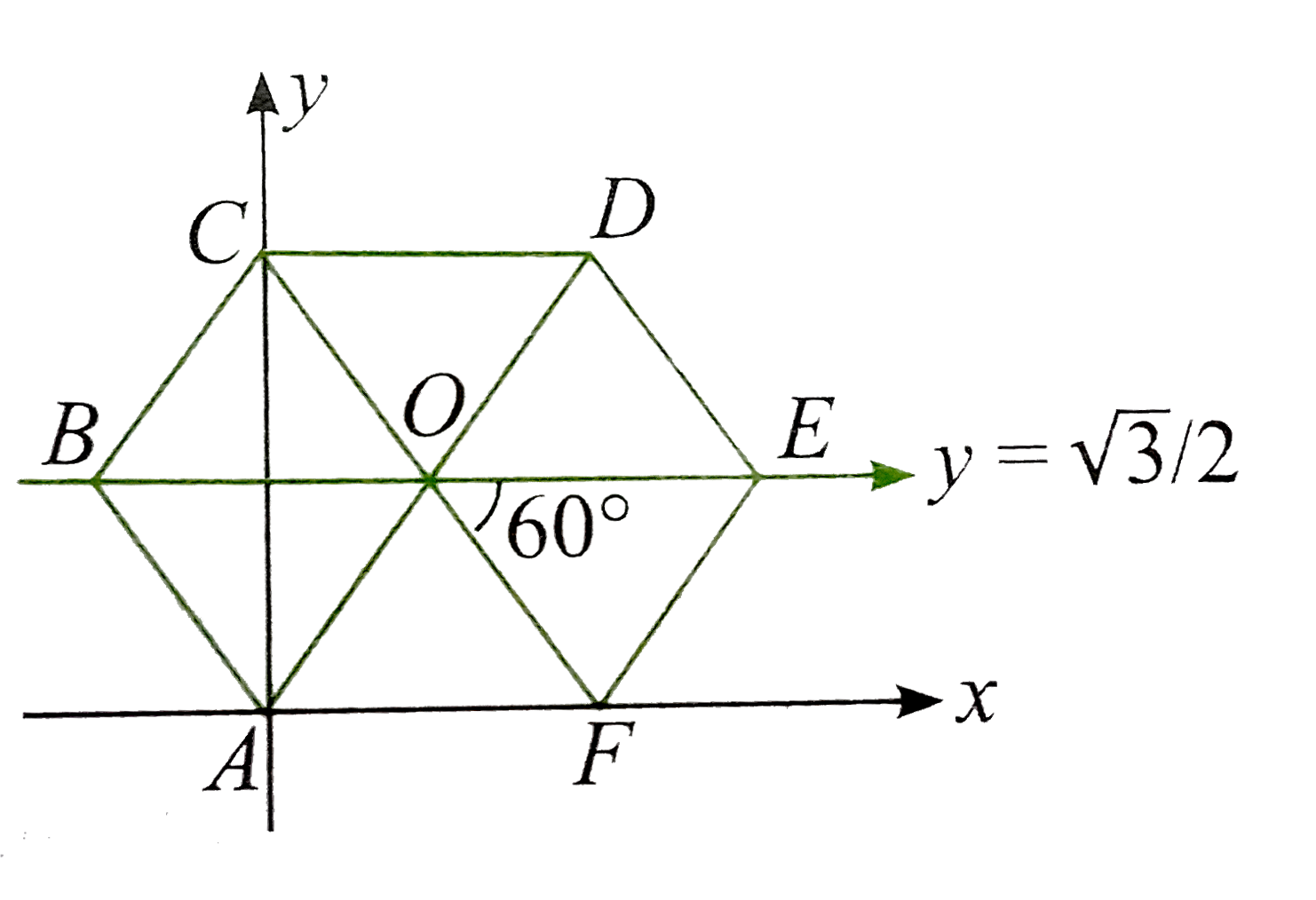
Two consecutive diagonals are the lines `sqrt(3)x = sqrt(3) " and " y= sqrt(3)//2.`
The angle between these two lines is `60^(@)`. As the polygon is regular, it will be a hexagon.
The center of the polygon is `(1//2, sqrt(3)//2), " and " (1,0) "lies on " sqrt(3) x + y = sqrt(3). " Hence,"`
`OF = sqrt(((1)/(2)-1)^(2) + ((sqrt(3))/(2))^(2)) = 1`
The equation of the third diagonal will be y `=sqrt(3)x`. The coordinates of the vertices are as follows:
`D(1,sqrt(3)), A(0,0), C(0,sqrt(3)), F(1,0),E(3//2, sqrt(3)//2), B(-1//2, sqrt(3)//2)`
The equations of the sides are
` overset(" "harr)(AF)-=y=0`
` overset(" "harr)(CD)-=y=sqrt(3)`
` overset(" "harr)(FE)-=y=sqrt(3)(x-1)`
` overset(" "harr)(AB)-=y=-sqrt(3)x`
` overset(" "harr)(BC)-=y=sqrt(3)(x+1)`
` overset(" "harr)(ED)-=y=-sqrt(3)(x-2)`