Question

A beam of light is sent along the line ${\displaystyle x-y=1}$
, which after refracting from the x-axis enters the opposite side by
turning through ${\displaystyle {30}^0}$
towards the normal at the point of incidence on the x-axis. Then the
equation of the refracted ray is
${\displaystyle (2-\sqrt{3})x-y=2+\sqrt{3}}$

${\displaystyle (2+\sqrt{3})x-y=2+\sqrt{3}}$

${\displaystyle (2-\sqrt{3})x+y=(2+\sqrt{3})}$

${\displaystyle y=(2-\sqrt{3})(x-1)}$

Options

A. `(2-sqrt(3))x-y=2+sqrt(3)`
B. `(2+sqrt(3))x-y=2+sqrt(3)`
C. `(2-sqrt(3))x+y=(2+sqrt(3))`
D. `y=(2+sqrt(3))(x-1)`

Answer

D

Explanation

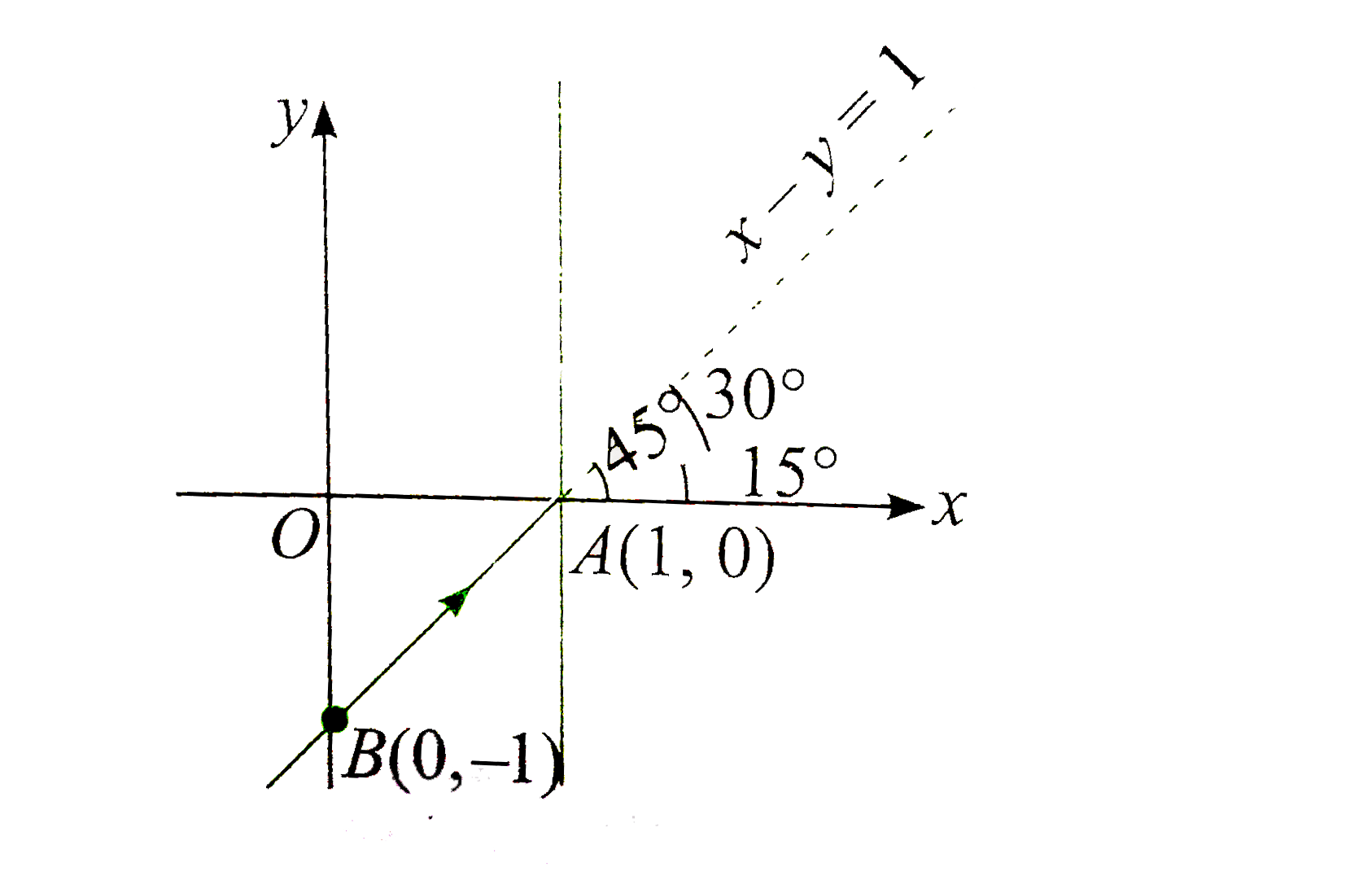
From the figure, the refracted ray makes and angle of `15^(@)` with the positive direction of the x-axis and passes through the point (1,0). Its equation is
`(y-0)=("tan" 15^(@))(x-1)`
`"or "y=(2-sqrt(3))(x-1)`