Doubtnut Promotions Sticky

Consider a ΔABC in which sides AB and AC are perpendicular to x-y-4=0 and 2x-y-5=0, repectively. Vertex A is (-2, 3) and the circumcenter of ΔABC is (3/2, 5/2).
The equation of the line in List I is of the form ax+by+c=0, where a,b,c∈I. Match it with the corresponding value of c in list II and then choose the correct code.
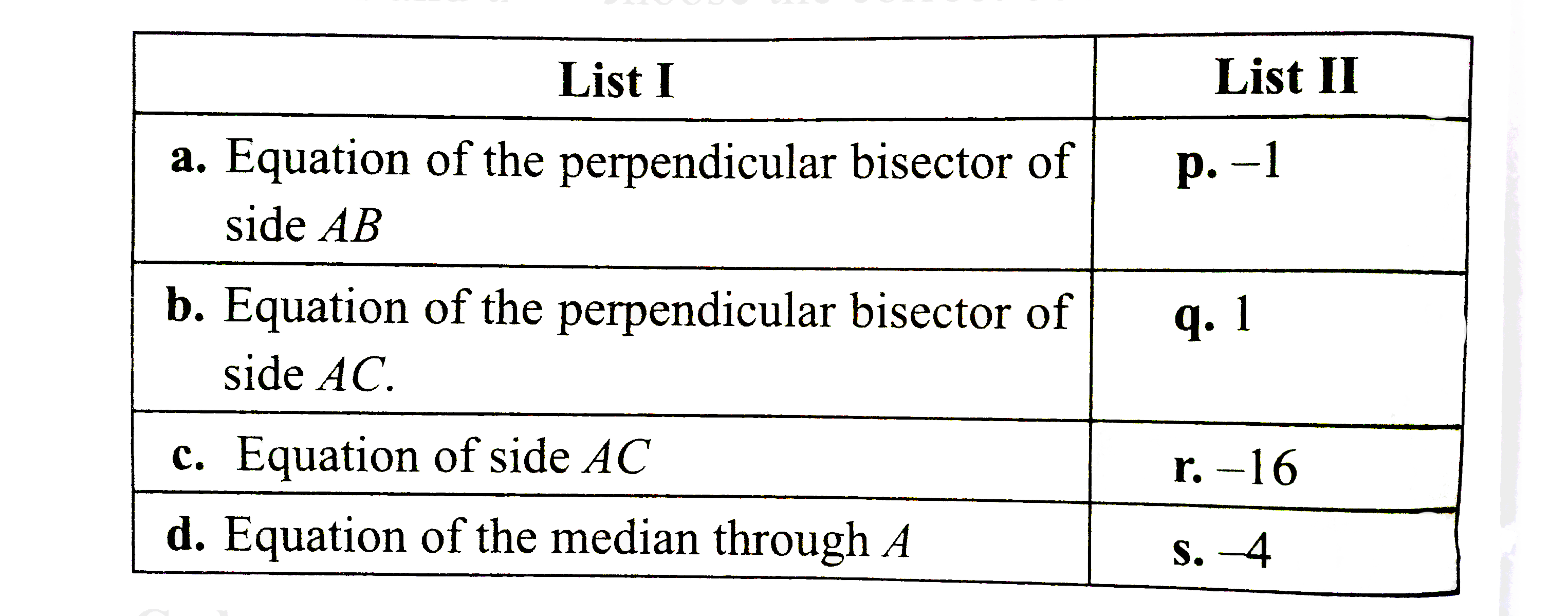
Consider a DeltaABC in which sides AB and AC are perpendicular to x-y-4=0 and 2x-y-5=0, repectively. Vertex A is (-2, 3) and the circumcenter of DeltaABC is (3/2, 5/2). The equation of the line in List I is of the form ax+by+c=0, where a,b,c in I. Match it with the corresponding value of c in list II and then choose the correct code. Codes : {:(a, b, c, d),(r, s, p, q),(s, r, q, p),(q, p, s, r),(r, p, s, q):}
Codes :
abcdrspqsrqpqpsrrpsq

Text Solution
Verified by Experts

The correct Answer is:3

a.
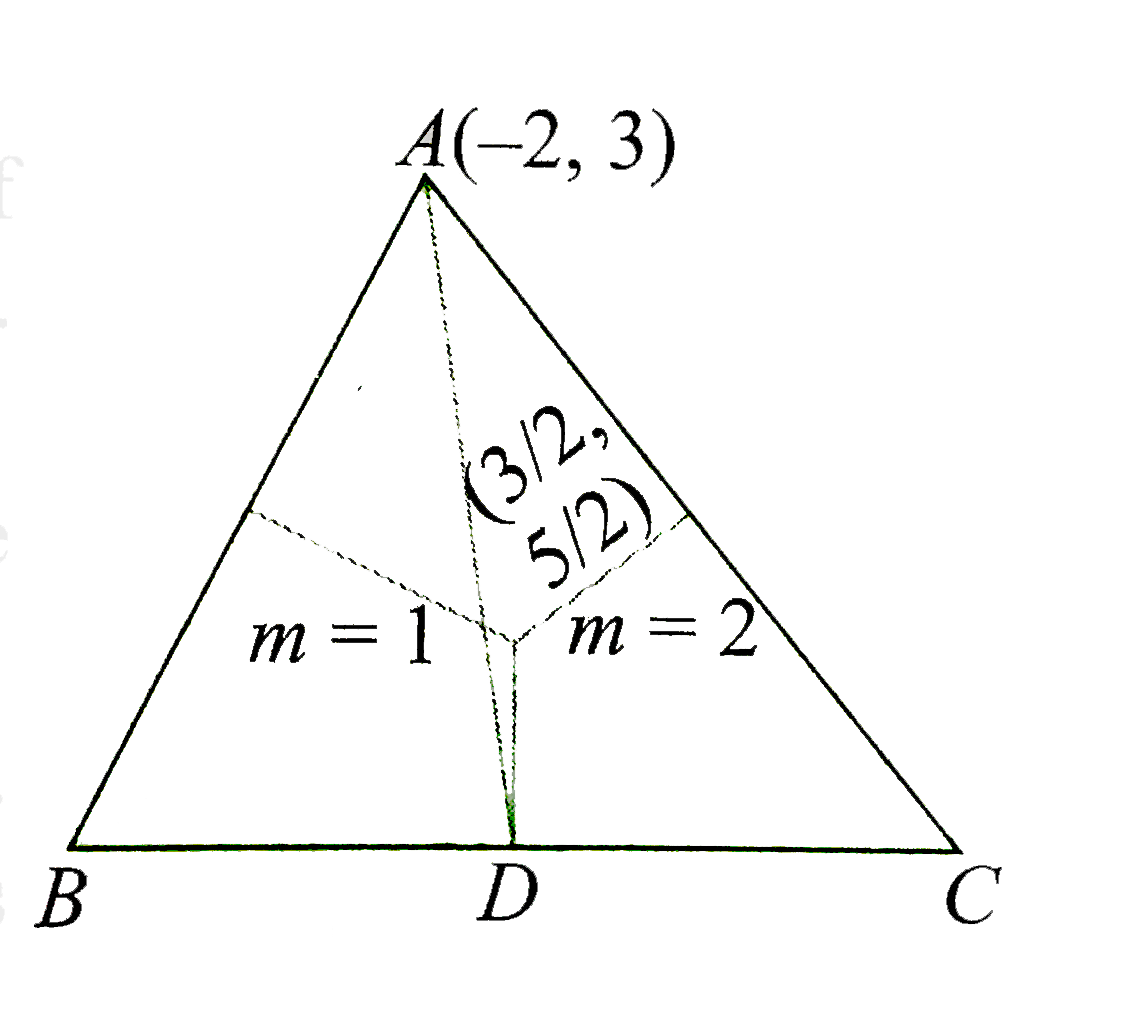
ocr_image
The perpendicular bisector of AB is parallel to x-y-4=0.
Therefore, the slope is 1.
It is passing through the circumcenter, i.e, (3/2, 5/2).
Therefore, the line is x-y+1 =0.
b. The perpendicular bisector of AC is B parallel to 2x-y-5=0.
Therefore, the slope is 2.
It is passing through the circumcenter, i.e., (3/2, 5/3).
Therefore, the line is 4x-2y-1=0.
c. The equation of perpendicular bisector to AC is 2x-y-5=0.
Therefore, the equation of AC can be x+2y+λ=0.
It is passing through A(-2, 3). Therefore,
λ=−4
Therefore, the equation of AC is x+2y-4=0.
d. The image of A on the perpendicular bisector of AC is
x+24=y−3−2=−2(−8−6−1)16+4=32
∴C≡(4,0)
The image of A on the perpendicular bisector of AB is
x+21=y−3−1=−2(−2−3+1)1+1=4
Therefore, B is (2, -1).
Therefore, the midpont of BC is D (3, -1/2).
Hence, the median through A is 7x+10y-16=0.

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let the equations of perpendicular bisectors of sides ACandofΔABCbex+y=3andx−y=1 respectively Then vertex A is is (0,0)
    The circumcentre of the ΔABC is

    A(1,1)
    B(2,1)
    C(0,0)
    D(0,1)
  • Question 2 - Select One

    Let the equations of perpendicular bisectors of sides ACandofΔABCbex+y=3andx−y=1 respectively Then vertex A is is (0,0)
    The orthocentre of ΔABC is

    A(1,1)
    B(2,1)
    C(0,0)
    D(0,1)
  • Question 3 - Select One

    The equations of perpendicular bisectors of the sides AB and AC of a ΔABC are x−y+5=0 and x+2y=0, respectively. If the point A is (1, - 2) the equation of the line BC is

    A23x+14y−40
    B23x+14y+40=0
    C14x+23y−40=0
    D14x+23y+40=0