Let a,b∈Qsuch that39√2−53−√2=a+b√2, then (A) √ba is a rational number (B) b and a are coprime rational numbers (C) b-a is a composite number (D) √a+b is a rational number
√ba is a rational number
b and a are coprime rational numbers
b-a is a composite number
√a+b is a rational number
Step by step video & image solution for Let a,b inQ"such that"(39sqrt2-5)/(3-sqrt2)=a+bsqrt2, then (A) sqrt((b)/(a)) is a rational number (B) b and a are coprime rational numbers (C) b-a is a composite number (D) sqrt(a+b) is a rational number by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If a and b are rational numbers a:b is equal to:
A−2:1B2:1C√3:1D−√3:1A rational number between √3and2
A1.8B0.8C1.66D1.5
Prove that √2 is not a rational number.
View SolutionFind rational numbers a and b such that .
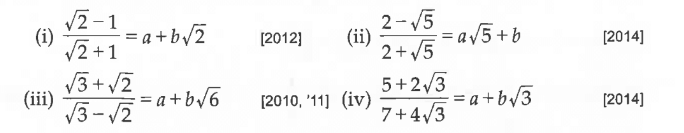
View SolutionIf 3+2√23−√2=a+b√2,"then a & b"(a, b inQ) are respectively equal to
View Solution√2 is a/an rational number (b) natural number irrational number (d) integer
View SolutionIf A & B are two rational numbers and AB, A + B and A -B are rational numbers, then A/B is :
View SolutionClassify : "True or False"
√2 is not a rational number.
View Solution
