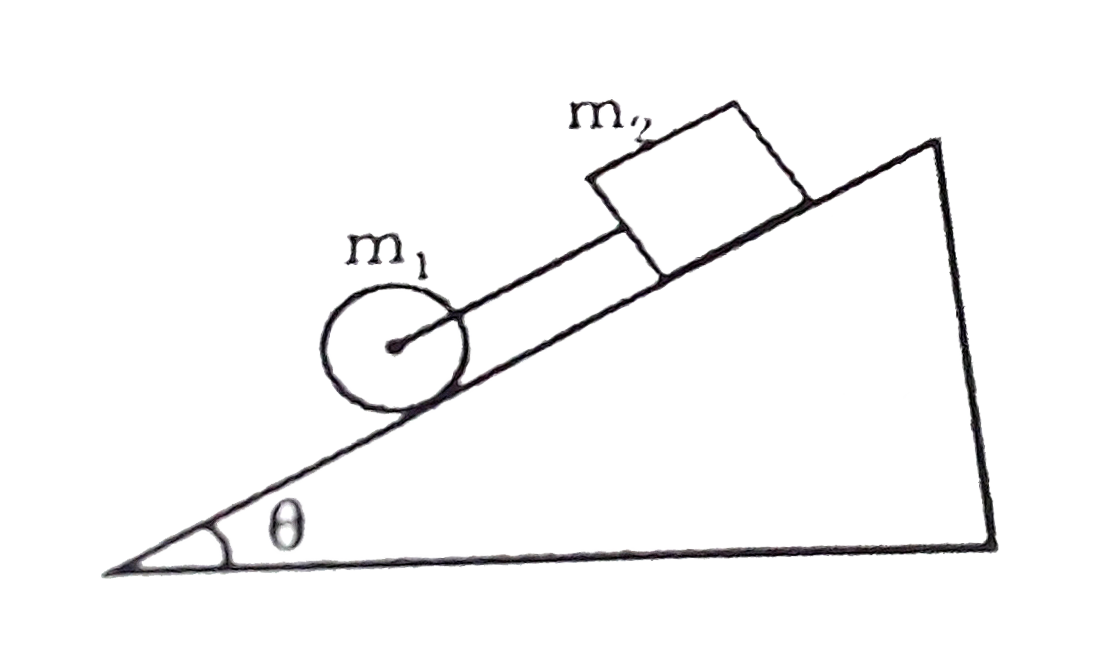
On an inclined plane making an angle theta with the horizontal plane,

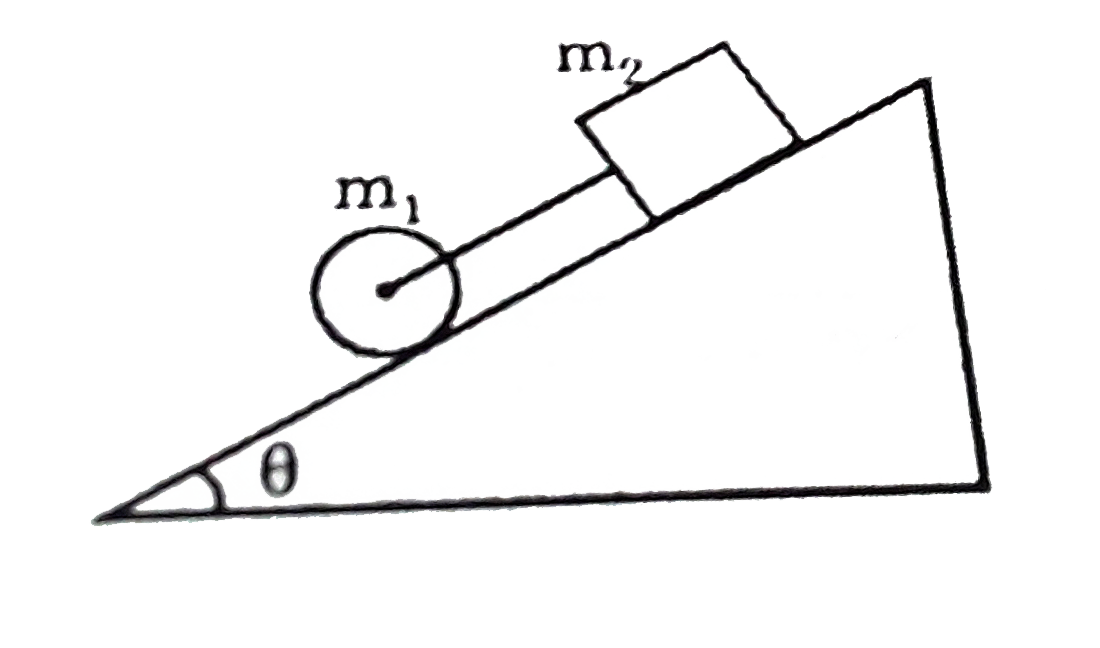
On an inclined plane making an angle $θ$ with the horizontal plane, a solid cylinder of mass $m_{1}$ is connected to a block of mass $m_{2}$ by means of a light chord which is parallel to incline plane . The coefficient of friction between block and incline and between cylinder and incline is equal to $μ$ . the system is held at rest & then released . If cylinder & block move together and cylinder perform pure rolling & tension in string is non zero then
Acceleration of block will be :

A $\frac{(m_{1} m_{2}) g sin θ - μ m_{2} g cos θ}{\frac{3}{2} m_{1} + m_{2}}$
B $\frac{(m_{1} m_{2}) g sin θ - μ m_{2} g cos θ}{\frac{3}{2} m_{1} + m_{2}}$
C $\frac{(m_{1} m_{2}) g sin θ - μ m_{2} g cos θ}{\frac{3}{2} m_{1} + 2 m_{2}}$
D $\frac{(m_{1} m_{2}) g sin θ - μ m_{2} g cos θ}{\frac{5}{2} m_{1} + m_{2}}$
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is $μ$ then
.
A $μ > tan θ$
B $f = m g sin θ$
C $f = μ m g cos θ$
Dthe reaction of the ground on the block is mg cos $θ$
A solid cylinder of mass $m$ and radius $r$ is rolling on a rough inclined plane of inclination $θ$ . The coefficient of friction between the cylinder and incline is $μ$ . Then.
Africtional force is always $μ m g cos θ$
Bfriction is a dissipative force
Cby decreasing $θ$ , frictional force decreases
Dfrictiona opposes translation and supports rotation.

The correct Answer is:D