A boat can be rowed at 5 m/s on still water. It is used to cross a 200m wide river from the south bank to the north bank. The river current has uniform velocity of 3 m/s due east.
(a) In which direction must it be steered to cross the river perpendicular to current ?
(b) How long will it take to cross the river in a direction perpendicular to the river flow ?
(c) In which direction must the boat be steered to cross the river in minimum time ? How far will it drift ?
(a) Velocity of a boat on still water is its capacity to move on water surface and equals to its velocity relative to water. →vb/w= Velocity of boat relative to water = Velocity of boat on still water
On flowing water, the water carries the boat along with it. Thus velocity →vb of the boat relative to the ground equals to vector sum of →vb/wand→vw. The boat crosses the river with the velocity →vb.
→vb=→vb/w+→vw

(b) To cross the river perpendicular to current the boat must be steered in a direction so that one of the components of its velocity (→vb/w) relative to water becomes equal and opposite to water flow velocity →vw to neutralize its effect. It is possible only when velocity of boat relative to water is greater than water flow velocity. In the adjoining figure its is shown that the boat starts from the point O and moves along the line OP (y-axis) due north relative to ground with velocity →vb. To achieve this it is steered at an angle θ with the y-axis.
vb/wsinθ=vw→5sinθ=3⇒θ=37∘

(c) The boat will cover river width b with velocity
vb=vb/wt=vb/wsin37∘=4m/s in time t, which is given by t=b/vb→t=50s
(d) To cross the river in minimum time, the component perpendicular to current of its velocity relative to ground must be kept to maximum value. It is achieved by steering the boat always perpendicular to current as shown in the adjoning figure. The boat starts from O at the south bank and reaches point P on the north bank. Time t taken by the boat is given by
t=b/vb/w→t=40s
Drift is the displacement along the river current measured from the starting point. Thus, it is given by the following equation. We denote it by xd
xd=vbxt
Substituting vbx=vw=3m/s, from the figure, we have
xd=120m
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?
View SolutionBoat moves with velocity 5 m/s on still water. It is steered perpendicular to the river current.
(a) Will it reach point B or somewhere else on the other bank ?
(b) How long will it take to cross the river?
(c) How far down stream, will it reach the other bank ?
(d) Does it take minimum time in this way ?
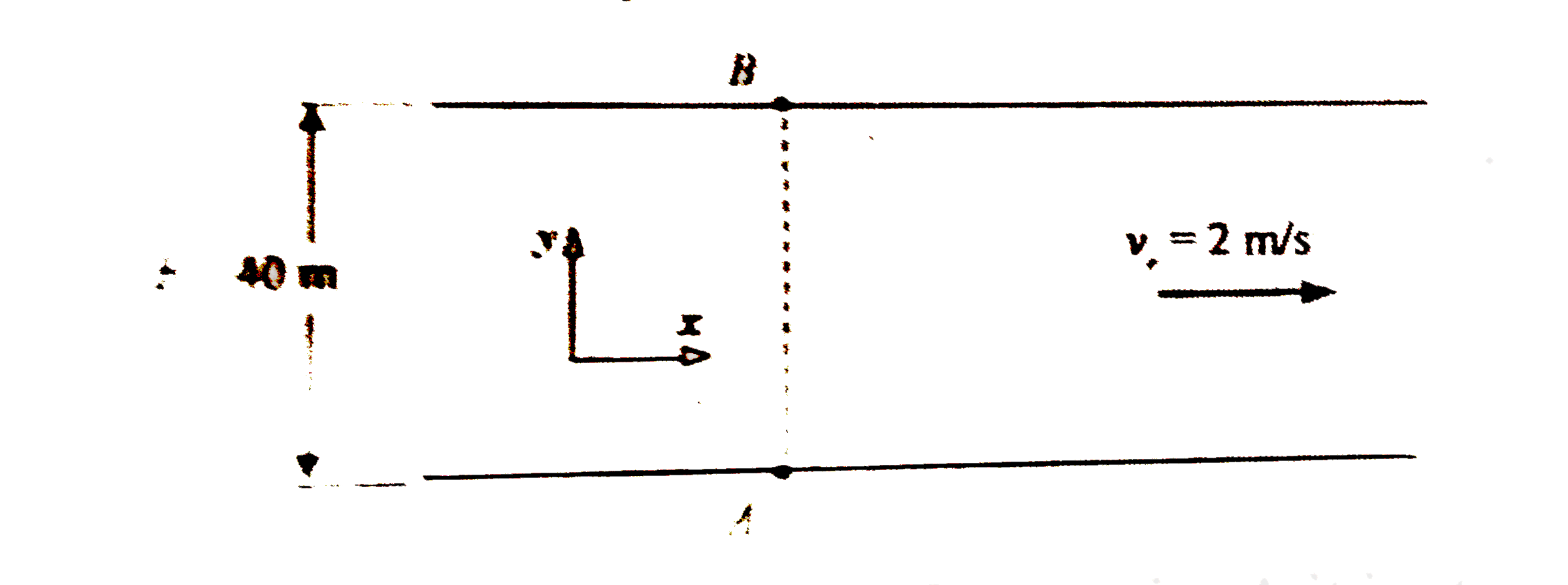
View Solution
Knowledge Check
A man can swim at 4 m/s in a still water swimming pool. He enters a 200 m wide river at one bank and swims ( w.r.t water) at an angle of 60∘ to the river flow velocity. The river flow velocity is 5 m/s . In how much -time does he cross the river ? Calculate his drift.
A200√3s,500√3mB100√3s,700√3mC50s, 1000 mD1000√3s,200√3mA man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
A120∘B150∘C30∘D60∘A man can swim in still water at a speed of 6kmph and he has to cross the river and reach just opposite point on the other bank.If the river is flowing at a speed of 3kmph,and the width of the river is 2km, the time taken to cross the river is (in hours)
A227B2√27C23D2√45
A river flows at 3 m/s and is 300 m wide . A man swing across the rivers with a velocity of 2 m/s directed always perpendicular to the flow of current . (a) How long does it take the man to cross the river ? (b) In what direction does he actually moves to cross the relative to the shore ? (c) How far down the fiver(from the starting point ) does he reach the opposite bank?
View SolutionA river is flowing from the west to the east at 5m/min. A swimmer on the southerm bank can swim at 10 m/min in still water. In what direction should he swim if (i) He wishes to cross the river in minimum time (ii) He wishes to cross te river through shortest route
View SolutionA river 600m wide wide flows at the rate of 8 km h^(-1). Still water, wishes to cross the river straight (i) Along what direction must be strike ? What will be his resultant velcity ? (ii) How much time he will take to cross the river ?
View SolutionA swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. His speed with respect to water is 3km/hr. (a) If the heads in a direction making an angle θ with the flow, he takes to cross the river. (b) Find the shortest possible time to cross the river.
View SolutionThe speed of boat is 5kmh−1 in still water. It crosses a river of width 1 km along the shortest possible path in 15 min. Then, velocity of river will be
View Solution
