Question

किसी h ऊँचाई के ऊर्ध्वाधर खम्भे के उच्चतम व न्यूतम बिन्दुओं से दो गोलियाँ क्रमशः $\alpha ={30}^{\circ }$ व $\beta ={60}^{\circ }$ के कोणों पर एक साथ छोड़ी जाती है व दोनों गोलियाँ किसी वस्तु से एक साथ टकराती है | यदि $a=30\sqrt{3}$, वस्तु की खम्भे से क्षैतिज दुरी है, तो खम्भे की ऊँचाई है

Options

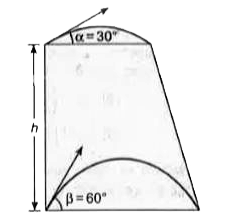
A. 30 मी
B. 45 मी
C. 60 मी
D. 90 मी

Answer

C

Explanation

`(v_(1)cos alpha)t = (v_(2)cos beta)t = a`
`therefore v_(1)=(a)/((cos alpha)t)` तथा `v_(2)=(a)/((cos beta)t) " "` ….(i)
पुनः `(v_(1)sin alpha)t-(1)/(2)g t^(2)+h`
`=(v_(2)sin beta)t-(1)/(2)g t^(2) " "` ....(ii)
समी (i) व (ii) से
`h=a(tan beta - tan alpha)`
`h=30sqrt(3){tan 60^(@)-tan 30^(@)}`
`=30sqrt(3){sqrt(3)-(1)/(sqrt(3))}=60` मी