एक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है | इससे R2 त्रिज्या का गोलीय भाग, आरेख में दर्शाए गए अनुसार काट लिया जाता है | r=α (अनन्त) पर गुरुत्वीय विभव के मान V को शून्य (V = 0) मानते हुए, इस प्रकार बने कोटर (कैविटी) के केन्द्र पर, गरुत्वीय विभव का मान होगा (G = गरुत्वीय स्थिरांक है)
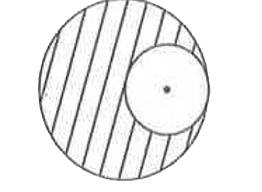
−2GM3R
−2GMR
−GM2R
−GMR
The correct Answer is:D
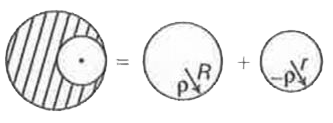
दिया है, गरुत्वीय विभव V = 0, जब r=∞ (अनन्त) ठोस गोले के अन्दर r दूरी पर गरुत्वीय विभव
V=−GMR[32−r22R2]
यहाँ, r=R2
V1=−GMR[32−(R/2)22R2]
=−GMR[32−R28R2]
=−GMR[12−18]
=−118GMR
जब r त्रिज्या के छोटे गोले को अलग कर लिया जाता है तो गरुत्वीय विभव,
V2=32.GM/8R/2=32×2GM8R
=38.GMR
कोटर अथवा कैविटी के केन्द्र पर कुल गरुत्वीय विभव,
V=V1+V2
=−118GMR+38GMR
=GMR[38−118]
=−GMR
Topper's Solved these Questions
Similar Questions
किसी निश्चित घटक के चुम्बकीय क्षेत्र के लिए सूत्र B=μ0NI2πr दिया गया है
जहाँ, N फेरों की कुल संख्या, i= प्रवाहित धारा तथा r =त्रिज्या है तो घटक है
View Solution4μF धारिता के तीन संधारित्र का संयोजन इस प्रकार करना है कि परिणामी धारिता 6μF हो | यह किस प्रकार किया जा सकता है ?
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionयदि किसी गोले का समीकरण x2+y2+z2+2ux+2vy+2wz+d=0 है, तो गोले के केन्द्र का निर्देशांक तथा त्रिज्या क्या होगी?
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (2,-3,4) तथा त्रिज्या 5 है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केन्द्र (2, 2, 1 ) तथा त्रिज्या 4 है।
View Solutionगरुत्वीय क्षेत्र तथा गरुत्वीय विभव
View SolutionIf the value of gravitational acceleration on the earth plane 10 मीटर/ Second ^ 2 है तो इसका मान प्रथ्वी के केन्द्र पर क्या होगा ( यदि प्रथ्वी को R त्रिज्या एंव एकसमान घनत्व का गोला मान लिया जाये)
View Solutionनिम्न को सुमेलित कीजिए
Aगरुत्वीय क्षेत्र तीव्रता pदीर्घवृत्तीय कक्षा में Bगरुत्वीय विभव qअर्ध दीर्घ अक्ष का गहन होता है Cसूर्य के चरों और परिक्रमण कर रहे ग्रहों के आवर्तकाल का वर्ग rग्रुत्वकरषण बल प्रति इकाई द्रव्यमान Dसभी ग्रह, सूर्य, के चरों और परिक्रमण कर रहे है sप्रति इकाई द्रव्यमान में किया गया कार्य
View Solution300 पर एक अभिक्रिया के लिए साम्य स्थिरांक 10 है| DeltaG^(ө) का मान क्या होगा ? R=8.314 JK^(-1) "mol"^(-1)
View SolutionA copper wire of radius 0.5 mm and length 4223 m is melted and converted into a sphere of radius R cm. What is the value of R?
त्रिज्या 0.5 mm और लंबाई 4223 मी वाले एक ताम्बे के तार को पिघलाकर त्रिज्या R सेमी वाले एक गोले का रूप दिया जाता है |R का मान क्या है ?
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
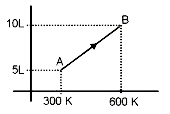
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionएक एकपरमाण्विक वास्तविक गैस का एक मोल समीकरण p (V — b) = RT को संतुष्ट करता है जहाँ b एक स्थिरांक है। गैस के लिए अंतरापरमाणुक विभव V(r) और अंतरापरमाणुक दूरी r का संबंध निम्नानुसार दर्शाया जाता है
View Solution25^(@)C पर एक सेल का मानक विद्युत वाहक बल 0.591 V पाया जाता है, जिसमें एक इलेक्ट्रॉन का परिवर्तन होता है। अभिक्रिया का साम्य स्थिरांक 10^(x) है। x का मान ज्ञात कीजिए।
View Solution
