द्रव की एक बूँद जिसका घनत्व है, द्रव जिसका घनत्व है, में आधा डूबा हुआ तैर रहा है। यदि द्रव का पृष्ठ तनाव s है, तो बूँद की त्रिज्या है
The correct Answer is:b
दिया है, द्रव की बूँद का घनत्व
द्रव का घनत्व जिसमें आधा डूबा हुआ तैर रहा है
द्रव का पृष्ठ तनाव = s
अब, द्रव बूँद पर कर्यरत बलों को सन्तुलित करने पर,
जहाँ, द्रव बूँद का भार,
द्रव बूँद पर कार्यरत उत्प्लावन बल
तथा द्रव बूँद पर कार्यरत पृष्ठ तनाव
तब,
या
या
या
या
या
या
या या
इसलिए, बूँद की त्रिज्या, होगी।
Topper's Solved these Questions
Similar Questions
4μF धारिता के तीन संधारित्र का संयोजन इस प्रकार करना है कि परिणामी धारिता 6μF हो | यह किस प्रकार किया जा सकता है ?
04:25View Solutionकोणीय संवेग मात्रा है
47:35View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
34:36View Solutionपरिचय |क्या द्रव विद्युत का चालन करते है ?
01:31:02View SolutionRevision|घनत्व क्या होता है |ठोस, द्रव तथा गैस के घनत्व की तुलना |निष्कर्ष |प्रश्न |अवस्था परिवर्तन |अवस्था परिवर्तन से संबंधित कुछ परिभाषाए |सारांश
52:08View Solutionठोस की द्रव में विलेयता, गैस की द्रव में विलेयता
03:26View Solutionद्रव स्थैतिकी द्रव गतिकी परिचय घनत्व दाब
View SolutionIn a U-tube, the radii of the two pillars are respectively r_1 " और " r_2 Huh. When rho (theta = 0^@) घनत्व का एक द्रव इसमें भरा जाता है, तो दो भुजाओं के स्तर में h | का अंतर देखा जाता है। द्रव का पृष्ठ तनाव है:
View Solutionएक द्रव, जल में अमिश्रणीय है जो कि 0.983 atm के दाब और 95.2^(@)C पर भाप आसवित है। आसुत में जल के प्रति ग्राम में उपस्थित द्रव का द्रव्यमान क्या है। द्रव का मोलर द्रव्यमान 134.3 g/mol है और जल का वाष्प दाब 0.84 atm है। साथ ही, शुद्ध द्रव का वाष्प दाब 0.143 atm है।
View Solution100°C और 1 atm पर यदि द्रव जल का घनत्व 1.0gcm−3 है और जल वाष्प का घनत्व 0.0006gcm−3 है, तब उसी ताप पर 1 लीटर भाप में जल के अणुओं द्वारा अधिकृत आयतन है-
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View SolutionNO_2 और N_2O_4 नाइट्रोजन डाइऑक्साइड के दो रूप हैं। एक गैसीय अवस्था में मौजूद होता है जबकि दूसरा द्रव अवस्था में। NO_2 और N_2O_4 रूपों की प्रकृति है:
View Solutionएक ठोस AB की NaCl प्रकार की संरचना है जिसकी कोर लम्बाई 580. 4 pm है। A+ की त्रिज्या 100 pm है। pm में B− की त्रिज्या क्या है?
View Solution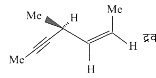
द्रव अमोनिया में सोडियम की उपस्थिति में उपरोक्त यौगिक का हाइड्रोजनीकरण देता है View Solutionएक ठोस XY में NaCl संरचना है। यदि X+ की त्रिज्या 100 pm है, तो Y आयन की त्रिज्या कितनी है?
View SolutionX' निम्न ताप पर पिघलता है और द्रव और ठोस दोनों अवस्थाओं में विद्युत् का कुचालक है। X है
View Solution