If the minimum value of the quadratic expression y=ax2+bx+c is negative attained at negative vlaue of x, then :
a>0
b>0
c>0
D>0
The correct Answer is:A, B, D
Step by step video, text & image solution for If the minimum value of the quadratic expression y =ax ^(2)+bx +c is negative attained at negative vlaue of x, then : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VK JAISWALCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)23videos
QUADRATIC EQUATIONS
- BOOK - VK JAISWALCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (MATCHING TYPE PROBLEMS)3videos
QUADRATIC EQUATIONS
- BOOK - VK JAISWALCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)45videos
QUADRATIC EQUATIONS
- BOOK - VK JAISWALCHAPTER - PROBABILITY EXERCISE - Exercise -5 : Subjective Type problems12videos
PROBABILITY
- BOOK - VK JAISWALCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)21videos
SEQUENCE AND SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One or More
The quadratic expression ax2+bx+c>0∀x∈R, then :
A13a−5b+2c>0B13a−b+2c>0Cc>0,D<0Da+c>b,D<0 - Question 2 - Select One
The values of 'a' for which the quadraic expression ax2+(a−2)x−2 is negative for exactly two integral values of x, belongs to
A[−1,1]B[1,2)C[−1,1]D[-2,-1]) - Question 3 - Select One
For which of the following graphs the quadratic expression y=ax2+bx+c the product abc is negative ?
A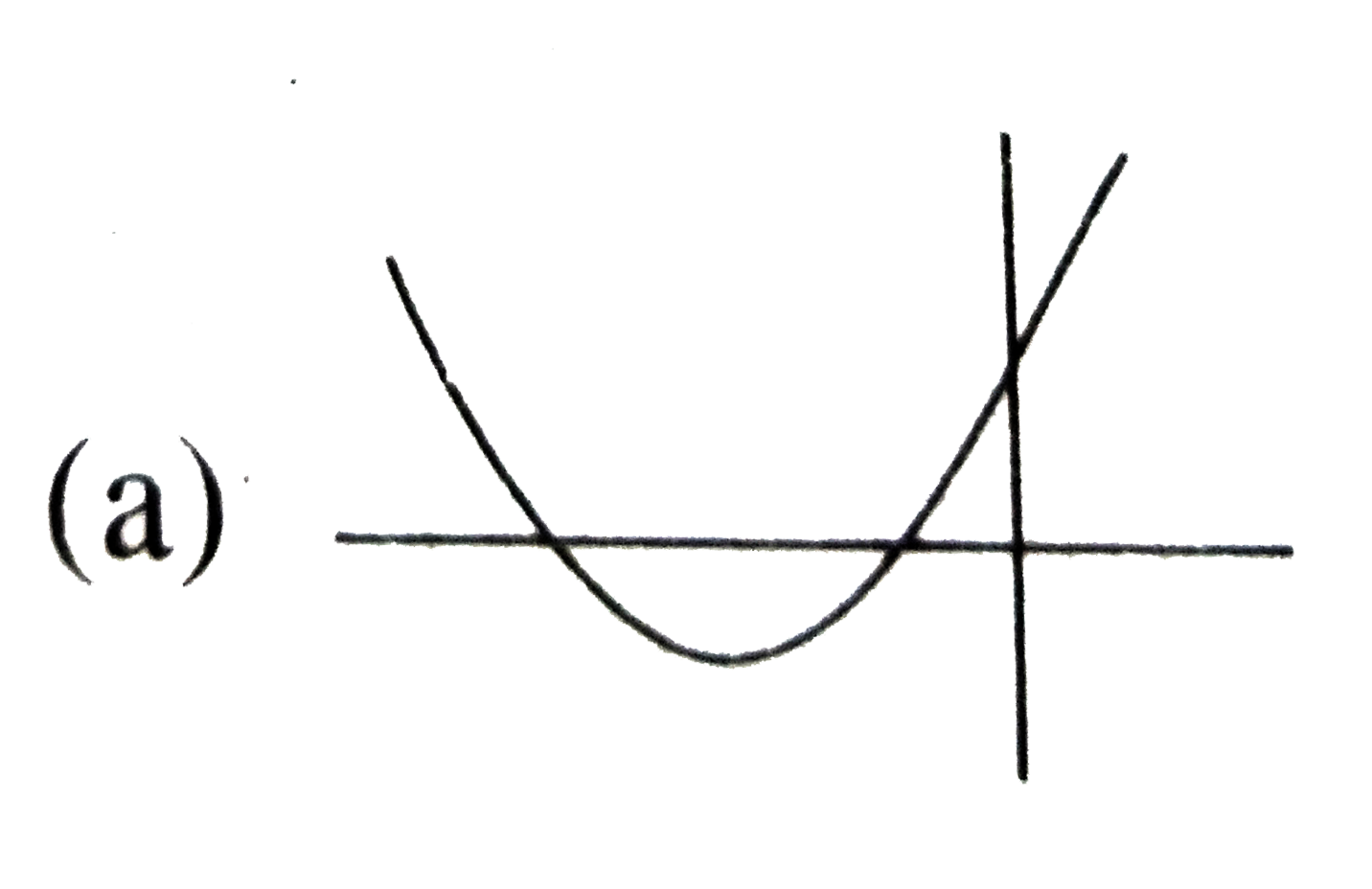 B
B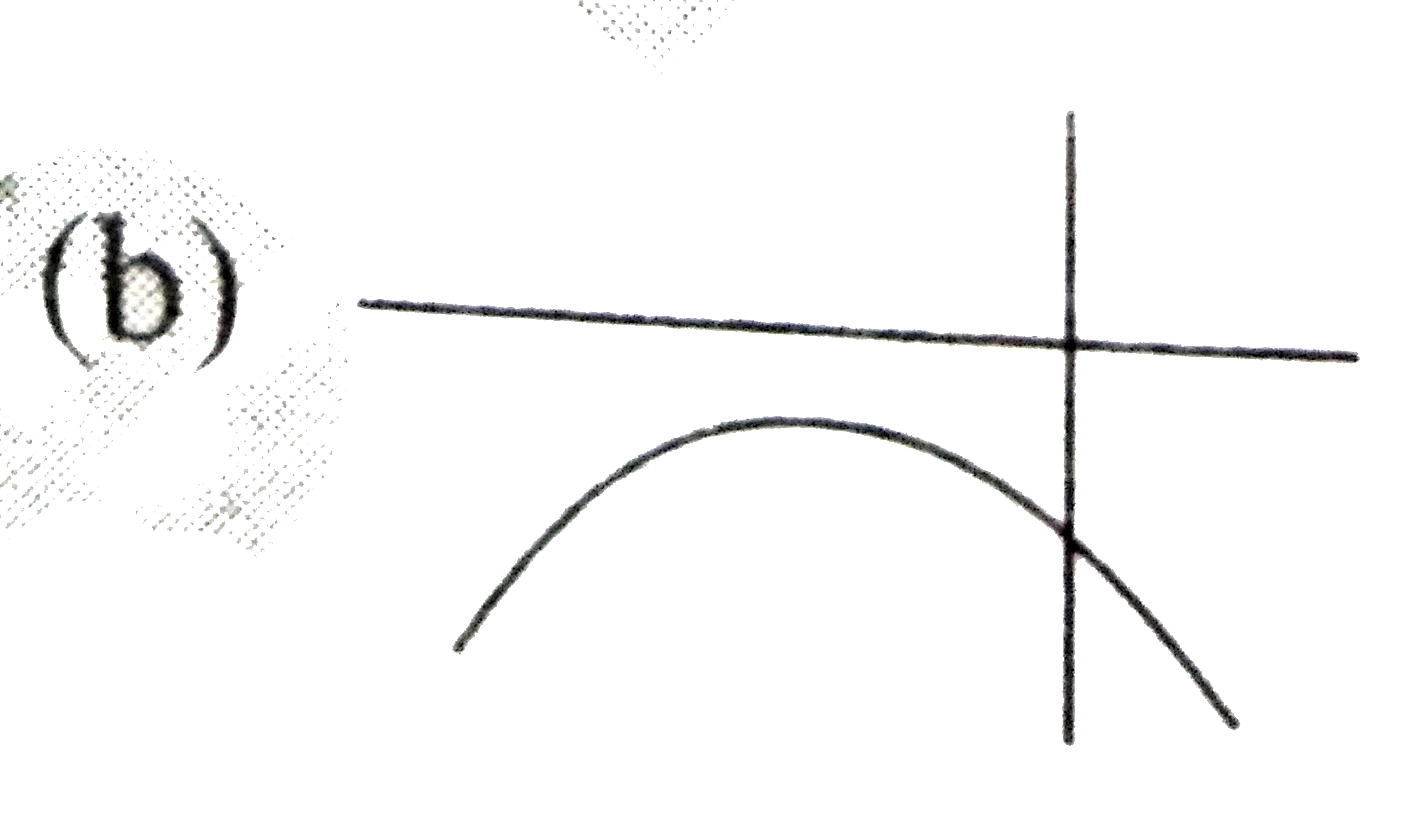 C
C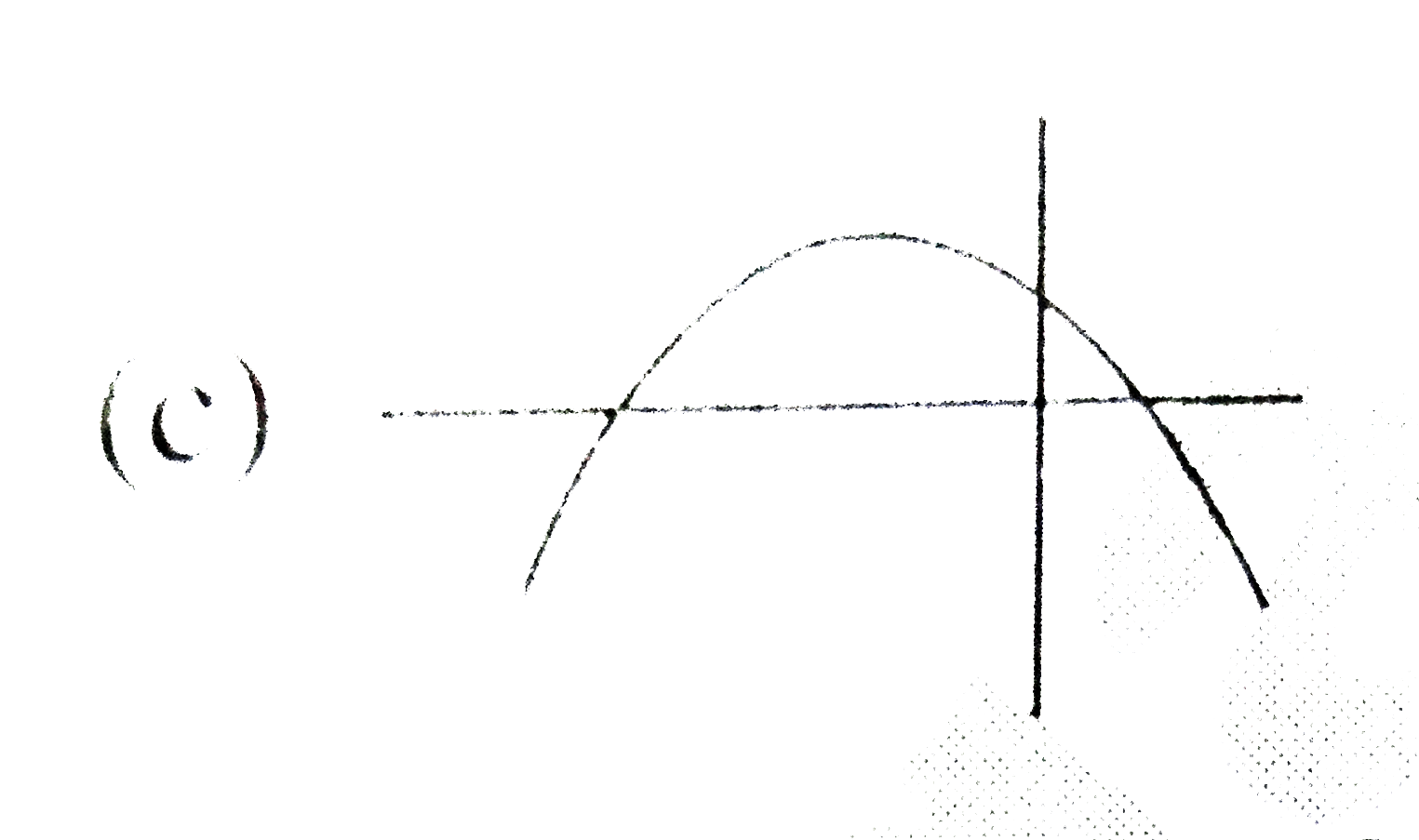 D
D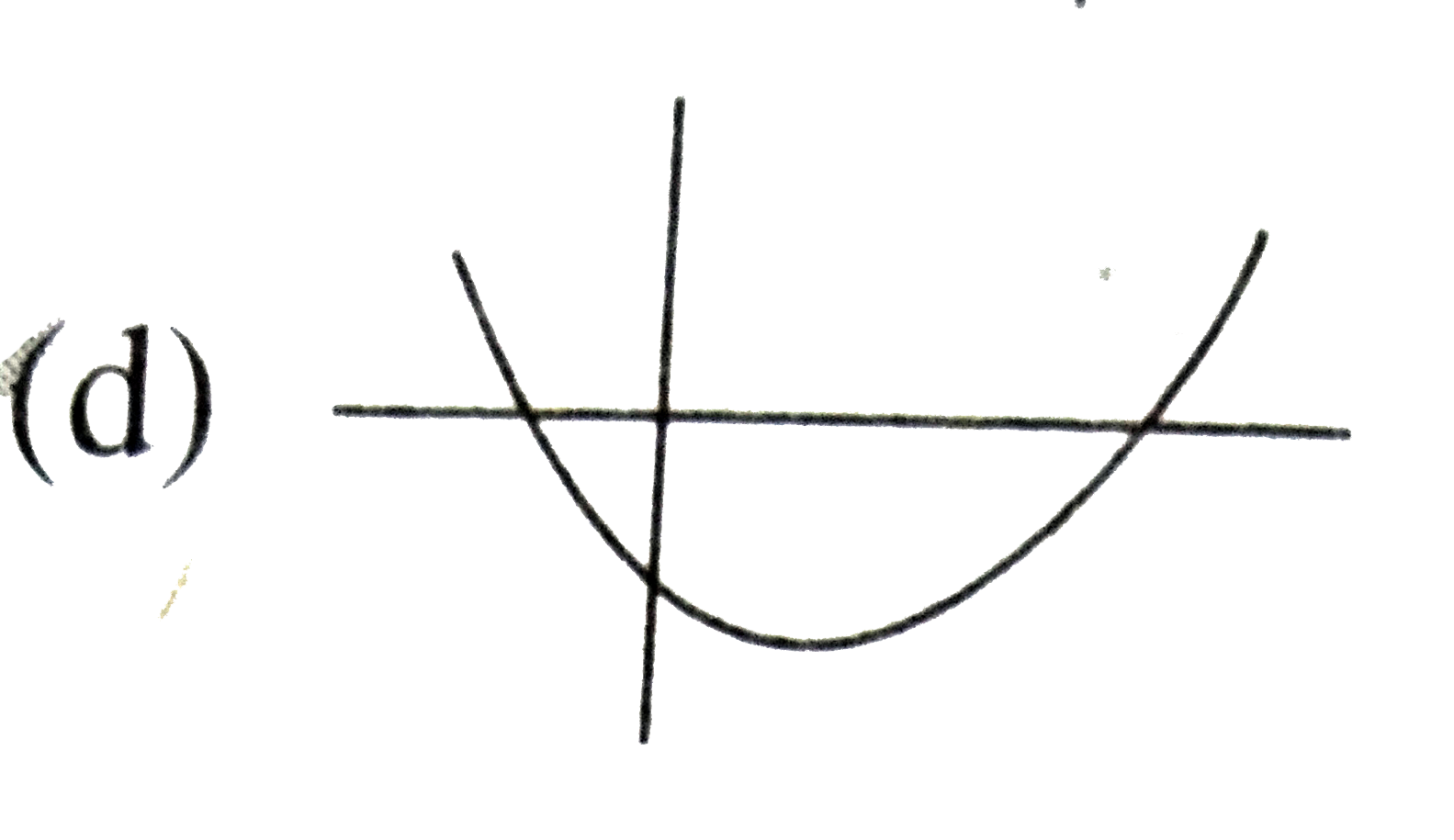
The quadratic expression ax2+bx+c>0 ∀x∈R ,then
View SolutionPlease explain Range of quadratic expression f(x)=ax2+bx+c
View SolutionThe values of 'a' for which the quadraic expression ax2+(a−2)x−2 is negative for exactly two integral values of x, belongs to
View SolutionIf a and b are the maximum and minimum values of the quadratic expressions 1−2x−5x2 and x2−2x+5 respectively then the set of the all values of x for which the expression 5ax2+bx+7 is positive
View SolutionIf graph of the quadratic y=ax2+bx+c is given below :
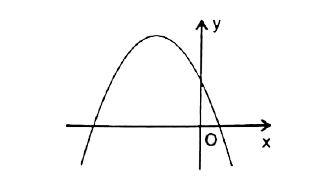 then: View Solution
then: View Solution

