A rod of AB of length 3 rests on a wall as follows :

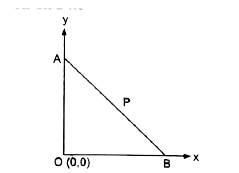
P is a point on AB such that $A P : P B = 1 : 2$ If the rod slides along the wall, then the locus of P lies on

$2 x + y + x y = 2$

$4 x^{2} + x y + x y + y^{2} = 4$

$4 x^{2} + y^{2} = 4$

$x^{2} + y^{2} - x - 2 y = 0$

Text Solution

Verified by Experts

The correct Answer is:C

Let ABCD be a square and let P be a point on AB such that $A P : P B = 1 : 2 . if ∠ A P D = θ$ , then what is the value of $cos θ$ ?
A $\frac{1}{\sqrt{10}}$
B $\frac{1}{\sqrt{5}}$
C $\frac{2}{\sqrt{10}}$
D $\frac{2}{\sqrt{5}}$
A point P moves such that PA/PB = p where A and B are two fixed pints with AB=a, the locus of P is a circle with radius
A $a . (1 - p^{2})$
B $p / (1 - a^{2})$
C $a p (1 - p^{2})$
D $a p / (1 - a^{2})$