Point P(p,0),Q(q,0),R(0,p),S(0,q) from parallelogram rhombus cyclic quadrilateral (d) none of these
To determine the type of quadrilateral formed by the points P(p,0), Q(q,0), R(0,p), and S(0,q), we can follow these steps:
Step 1: Identify the Points
The points given are:
- P(p,0) - This point lies on the x-axis.
- Q(q,0) - This point also lies on the x-axis.
- R(0,p) - This point lies on the y-axis.
- S(0,q) - This point also lies on the y-axis.
Step 2: Plot the Points
We can plot these points on a Cartesian coordinate system:
- P is at (p,0)
- Q is at (q,0)
- R is at (0,p)
- S is at (0,q)
Step 3: Analyze the Shape
To analyze the shape formed by these points:
1. Connect the Points: Draw lines connecting P to R, R to Q, Q to S, and S back to P.
2. Check the Angles:
- The angles at P and Q are both 90∘ since they are on the x-axis.
- The angles at R and S are also 90∘ since they are on the y-axis.
Step 4: Determine the Type of Quadrilateral
Since we have:
- Opposite angles that are equal (both pairs of opposite angles are 90∘).
- The lengths of the sides are equal if p=q.
This indicates that the quadrilateral is a rectangle. However, we need to check if it is a cyclic quadrilateral.
Step 5: Check for Cyclic Properties
A quadrilateral is cyclic if the sum of each pair of opposite angles is 180∘:
- 90∘+90∘=180∘
- 90∘+90∘=180∘
Since both pairs of opposite angles sum to 180∘, the quadrilateral is also cyclic.
Conclusion
The quadrilateral formed by the points P(p,0), Q(q,0), R(0,p), and S(0,q) is a cyclic quadrilateral.
---
The points given are:
- P(p,0) - This point lies on the x-axis.
- Q(q,0) - This point also lies on the x-axis.
- R(0,p) - This point lies on the y-axis.
- S(0,q) - This point also lies on the y-axis.
We can plot these points on a Cartesian coordinate system:
- P is at (p,0)
- Q is at (q,0)
- R is at (0,p)
- S is at (0,q)
To analyze the shape formed by these points:
1. Connect the Points: Draw lines connecting P to R, R to Q, Q to S, and S back to P.
2. Check the Angles:
- The angles at P and Q are both 90∘ since they are on the x-axis.
- The angles at R and S are also 90∘ since they are on the y-axis.
Since we have:
- Opposite angles that are equal (both pairs of opposite angles are 90∘).
- The lengths of the sides are equal if p=q.
A quadrilateral is cyclic if the sum of each pair of opposite angles is 180∘:
- 90∘+90∘=180∘
- 90∘+90∘=180∘
The quadrilateral formed by the points P(p,0), Q(q,0), R(0,p), and S(0,q) is a cyclic quadrilateral.
Similar Questions
Knowledge Check
Four charges +q,+q−q, and -q are placed on X - Y plane at the points whose coordinates are (0.5,0),(0,0.5),(−0.5,0)and(0,−0.5) respectively.
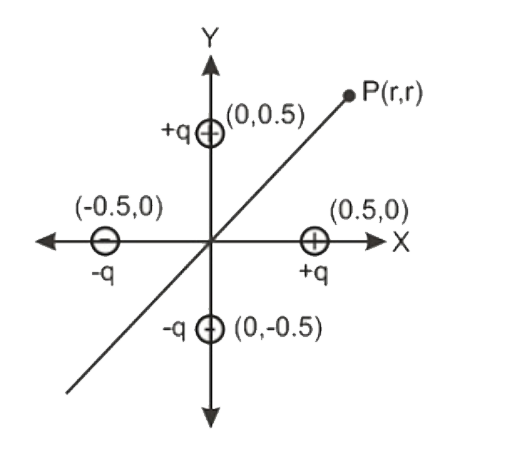
The electric field due to these charges at a point P(r,r), where r>>0.5, will beA14πε0×q2r3B14πε0×qr3C14πε0×3qr3D1πε0×qr3∣∣ ∣ ∣∣0p−qp−rq−q0q−rr−pr−q0∣∣ ∣ ∣∣ is equal to
A0B(p−q)(q−r)(r−p)CpqrD3pqrThree charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
A14πε0qa2r4B14πε02qa2r3C14πε04qa2r2D14πε08qa2r
If the points (0,0),(2,2√3),and(p,q) are the verticesof an equilateral triangle, then (p,q) is
View SolutionThe points (p,q +r) , (q, r+p) and (r, q+p) are _______.
View SolutionIf p>1 and q>1 are such that log(p+q)=logp+logq,then the value of log(p−1)+log(q−1) is equal to (a) 0 (b) 1 (c) 2 (d) none of these
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionIf the numbers p,q,r are in A.P. then m7p,m7q,m7r(m>0) are in (A) A.P. (B) G.P. (C) H.P. (D) none of these
View Solution
