The equation of a line through the point (1, 2) whose distance from the point (3,1) has the greatest value is (a)y=2x (b) y=x+1 (c)x+2y=5 (d) y=3x−1
y=2x
y=x+1
x+2y=5
y=3x-1
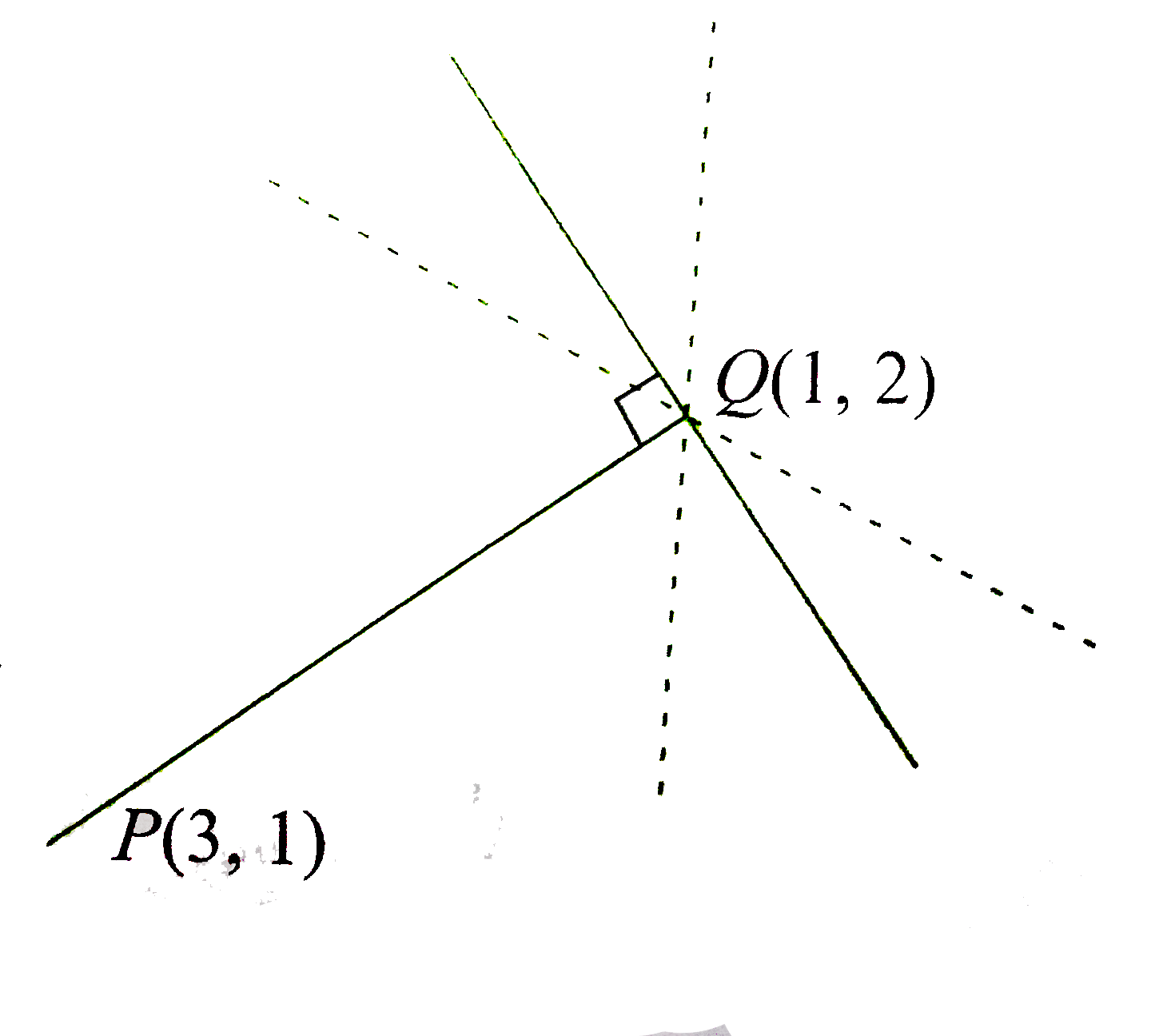
Obviously, the line through Q is at the greatest distance from point P when it is perpendicular to PQ. Now, the slope of line PQ is mPQ=−1/2. Then the slope of perpendicular line passing through Q is
y-2 = 2(x-1)
or 2x-y=0
Similar Questions
Knowledge Check
- Question 1 - Select One
Equation to the curve through (2, 1) whose slope at the point (x, y) is (x2+y2)/2xy is
A2(x2−y2)=3xB2(y2−x2)=6yCx(x2−y2)=6DNone of these
Find the equation of the line through point (1,2,3) and parallel to line x−y+2z5,3x+y+z=6.
View SolutionThe distance of the line 2x−3y=4 from the point (1, 1) in the direction of the line x+y=1 is
View SolutionThe equation of the curve through the point (3,2) and whose slope is x2y+1, is (A) 1 (B) 2 (C) 3 (D) 4
View SolutionWhat are the points on y-axis whose distance from the line x3+y4=1 is 2 units
View SolutionThe equation of the locus of points which are equidistant from the points (2,-3) and (3,-2) is
(A) x+y=0
(B) x+y=7
(C) 4x+4y=38
(D) x+y=1View SolutionThe equation of the straight line through the point of intersection of lines x-3y+1=0 and 2x+5y-9=0 and whose distance from the origin is 5
View SolutionEquation of the line through the point of intersection of the lines 3x+2y+4=0and2x+5y−1=0 whose distance from (2,−1) is 2.
View Solution

