The energy levels of a hypothetical one - electron atom system are given by , where . The wavelength of emitted photom corresponding to the transitition from first excited level to ground level is about
1035 Å
1220 Å
3650 Å
690 Å
The correct Answer is:A
To solve the problem, we need to find the wavelength of the emitted photon corresponding to the transition from the first excited level (n=2) to the ground level (n=1) in a hypothetical one-electron atom system with energy levels given by En=16n2 eV.
1. Identify the Energy Levels:
- For the ground state (n=1):
E1=1612=16 eV
- For the first excited state (n=2):
E2=1622=164=4 eV
2. Calculate the Energy Difference:
- The energy difference ΔE when the electron transitions from n=2 to n=1 is given by:
ΔE=E1−E2=16 eV−4 eV=12 eV
3. Use the Energy-Wavelength Relation:
- The energy of a photon is related to its wavelength by the formula:
E=hcλ
- Rearranging this gives:
λ=hcE
- Alternatively, using the shortcut formula for energy in eV:
λ(in angstrom)=12420E(in eV)
4. Substituting the Energy:
- Now substituting E=12 eV into the shortcut formula:
λ=1242012
5. Calculating the Wavelength:
- Performing the division:
λ=1035 angstrom
Final Answer:
The wavelength of the emitted photon corresponding to the transition from the first excited level to the ground level is approximately 1035 angstrom.
- For the ground state (n=1):
E1=1612=16 eV
- For the first excited state (n=2):
E2=1622=164=4 eV
- The energy difference ΔE when the electron transitions from n=2 to n=1 is given by:
ΔE=E1−E2=16 eV−4 eV=12 eV
- The energy of a photon is related to its wavelength by the formula:
E=hcλ
- Rearranging this gives:
λ=hcE
- Alternatively, using the shortcut formula for energy in eV:
λ(in angstrom)=12420E(in eV)
- Now substituting E=12 eV into the shortcut formula:
λ=1242012
- Performing the division:
λ=1035 angstrom
The wavelength of the emitted photon corresponding to the transition from the first excited level to the ground level is approximately 1035 angstrom.
Topper's Solved these Questions
Similar Questions
The energy levels of a hypothetical one electron atom are given by En=−18.0n2eV
where n = 1,2,3,…. (a) Compute the four lowest energy levels and construct the energy levels diagram. (b) What is the first excitation potential (c ) What wavelength (Å) can be emitted when these atoms in the ground state are bombarged by electrons that have been accelerated through a potential difference of 16.2 V? (e) what is the photoelectric threshold wavelength of this atom?
View SolutionThe energy levels of a hypothetical one electron atom are given
En=−18.0n2eV, where n=1,2,3 …
a Cumpete the four lowest energy levels and construct the energy level diagram .
b What is the excitation potential of the state n=2?
c What wavelengths (Å) can be emitted when these atoms in the ground stste are bombarded by electron that have been accelerate through a potential difference of 16.2V
d If these atoms are in the ground state , can they absorb radiation having a wavelength of 2000Å ?
e what is the photoclectric threshold wavelength of this atom ?
View Solution
Knowledge Check
The energy levels of a hypotherical one electron atom are shown in figure
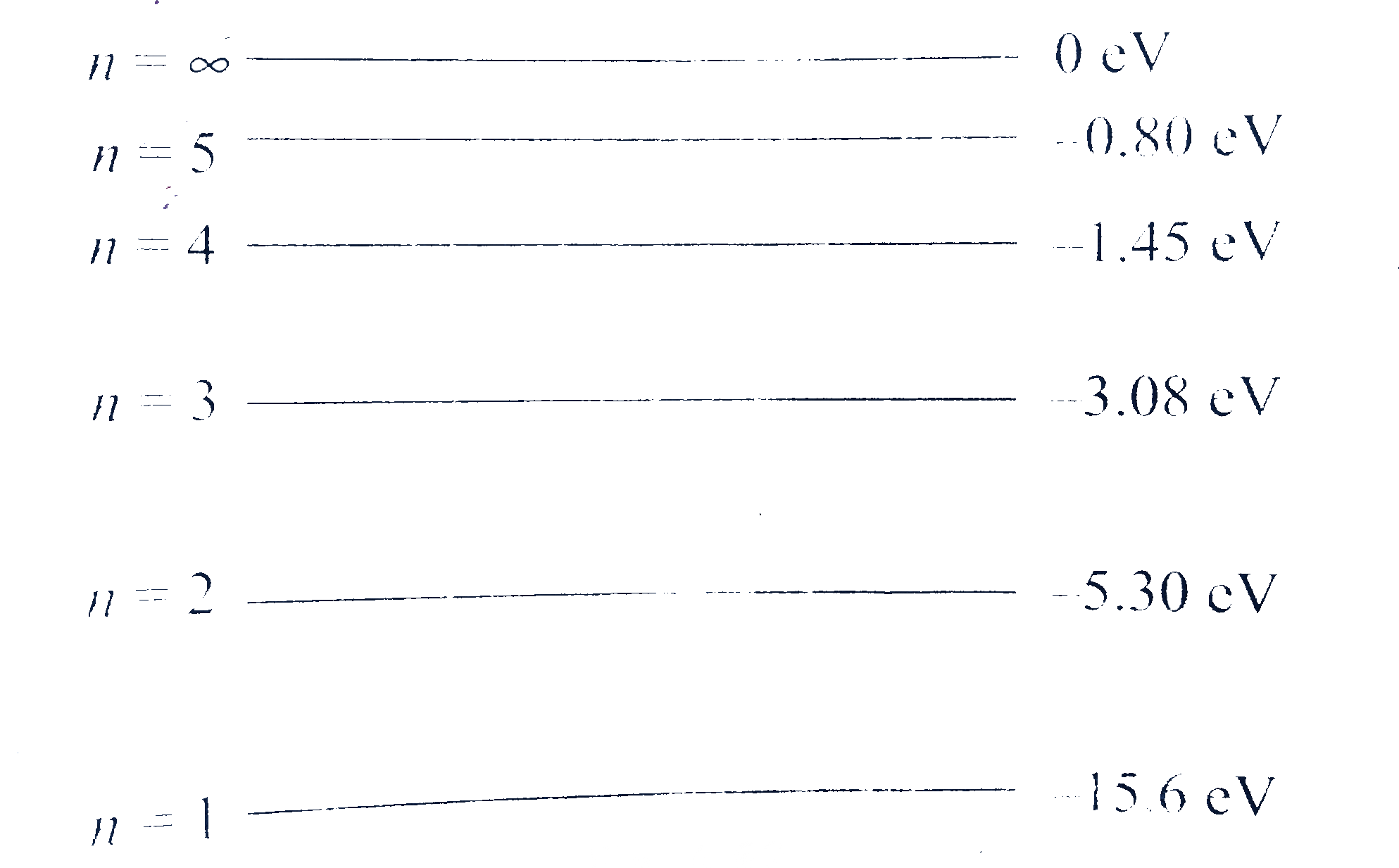
Find the excitation potential for the state n=3.A14.64eVB9.93eVC12.52eVD10.04eVThe energy levels of a hypotherical one electron atom are shown in figure
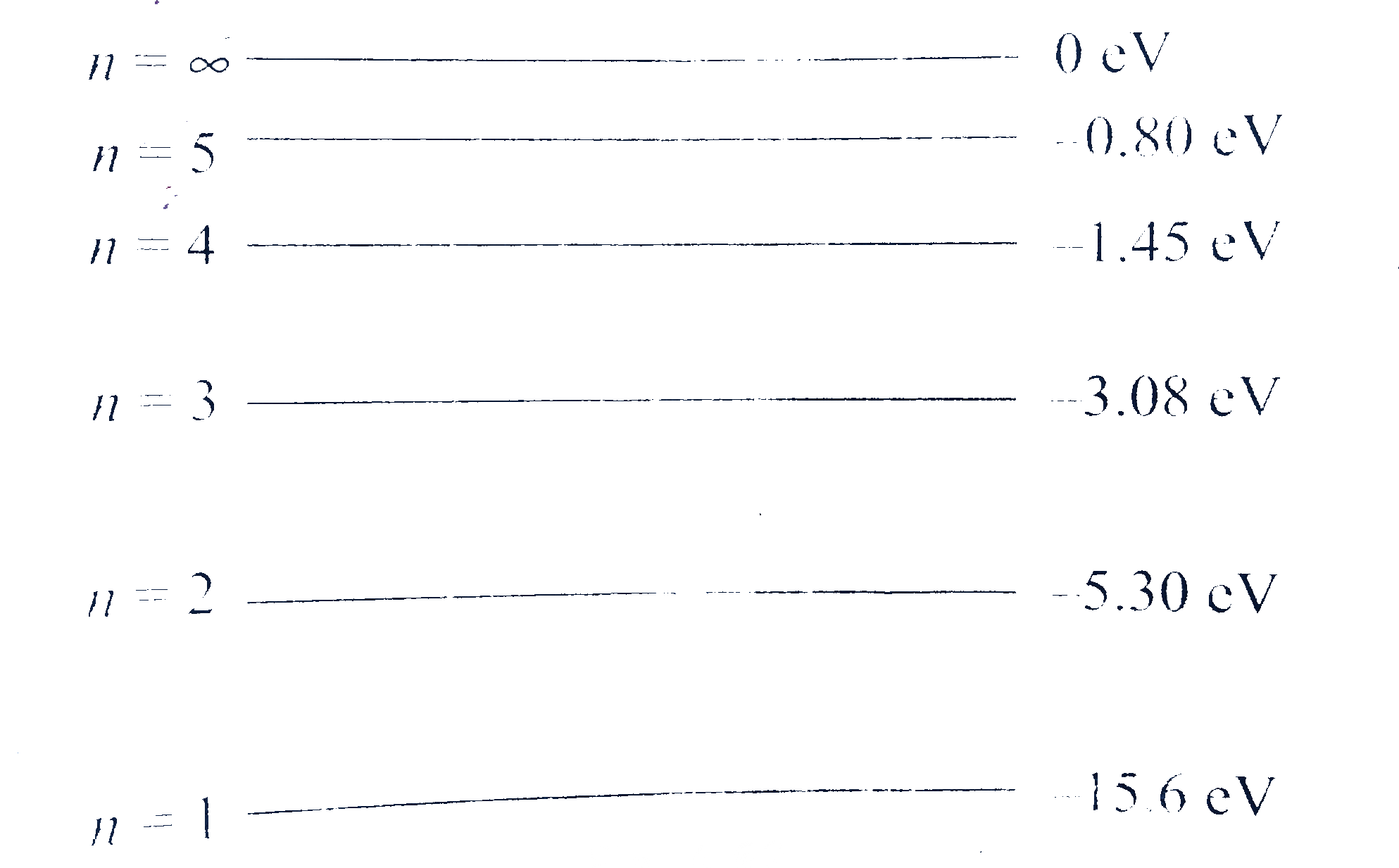
Find the wave number of the photon emitted for the transition n=3→n=1A2.23×107m−1B1.009×107m−1C3.005×106m−1D0.432×106m−1The energy levels of a hypotherical one electron atom are shown in figure

Find the short wavelength limit of the series terminating at n=2.A3256ÅB2339ÅC2509ÅD3494Å
A monochromatic light of frequency is incident on a metal surface and ejects photoelectrons. The photoelectrons having maximum kinetic energy are just able to ionise a hypothetical atom in ground state. The energy levels of hypothetical one-electron atom' are given by En=−29n2eV, where n = 1,2,3.....When whole experiment is repeated with an incident light of frequency v/2, the photoelectrons with maximum kinetic energy are just able to ionise hydrogen atom in ground state. Calculate the work function of the metal
View Solutionwhat is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n=4 to and energy level with n=2 ?
View SolutionWhat is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from the energy level with n=4 to the energy level with n=1 ?
View SolutionThe energy levels of a hypothetical one electron atom are shown in the figure. (a)Find the ionization potential of this atom.
(b) Find the short wavelength limit of the series terminating at n=2
(c ) Find the excitaion potential for the state n=3.
(d) find wave number of the photon emitted for the transiton n=3 to n=1 ∝__________0eV
n=5____________−0.80eV
n=4 ______________ -1.45 eV<br>n=3____________−3.08eV
n=2_______________ -5.30 eV<br>n=1 ____________________ -15.6 eV.
View SolutionCalculate the wavelength of radiation emited when an electron in a hydrogen atom makes a transition from an energy level with n=3 to a level with n=2
View Solution
