Four sound sources produce the following four waves
(i) $y_{1} = a sin (ω t + ϕ_{1})$
(ii) $y_{2} = a sin 2 ω t$
(iii) $y_{3} = a' sin (ω t + ϕ_{2})$
(iv) $y_{4} = a' sin (3 ω t + ϕ)$
Superposition of which two waves gives rise to interference?

(i) and (ii)

(ii) and (iii)

(i) and (iii)

(iii) and (iv)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Four sound sources produce the following four waves (i) y_(1)=a sin (omega t+phi_(1)) (ii) y_(2)=a sin 2 omega t (iii) y_(3)= a' sin (omega t+phi_(2)) (iv) y_(4)=a' sin (3 omega t+phi) Superposition of which two waves gives rise to interference? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS NTA NEET SET 115

Topper's Solved these Questions

Knowledge Check

Four sound sources produce the following four waves
(i) $y_{1} = a sin (ω t + ϕ_{1})$
(ii) $y_{2} = a sin 2 ω t$
(iii) $y_{3} = a' sin (ω t + ϕ_{2})$
(iv) $y_{4} = a' sin (3 ω t + ϕ)$
Superposition of which two waves gives rise to interference?
A(i) and (ii)
B(ii) and (iii)
C(i) and (iii)
D(iii) and (iv)
Four different independent waves are represented by
(i) $y_{1} = a_{1} sin ω t$ , (ii) $y_{2} = a_{2} sin 2 ω t$
(iii) $y_{3} = a_{3} cos ω t$ , (iv) $y_{4} = a_{4} sin (ω t + \frac{π}{3})$
With which two waves interference is possible
AIn (i) and (iii)
BIn (i) and (iv)
CIn (iii) and (iv)
DInsufficient data to predict.
If $i_{1} = i_{0} sin (ω t), i_{2} = i_{0_{2}} sin (ω t + ϕ)$ , then $i_{3} =$

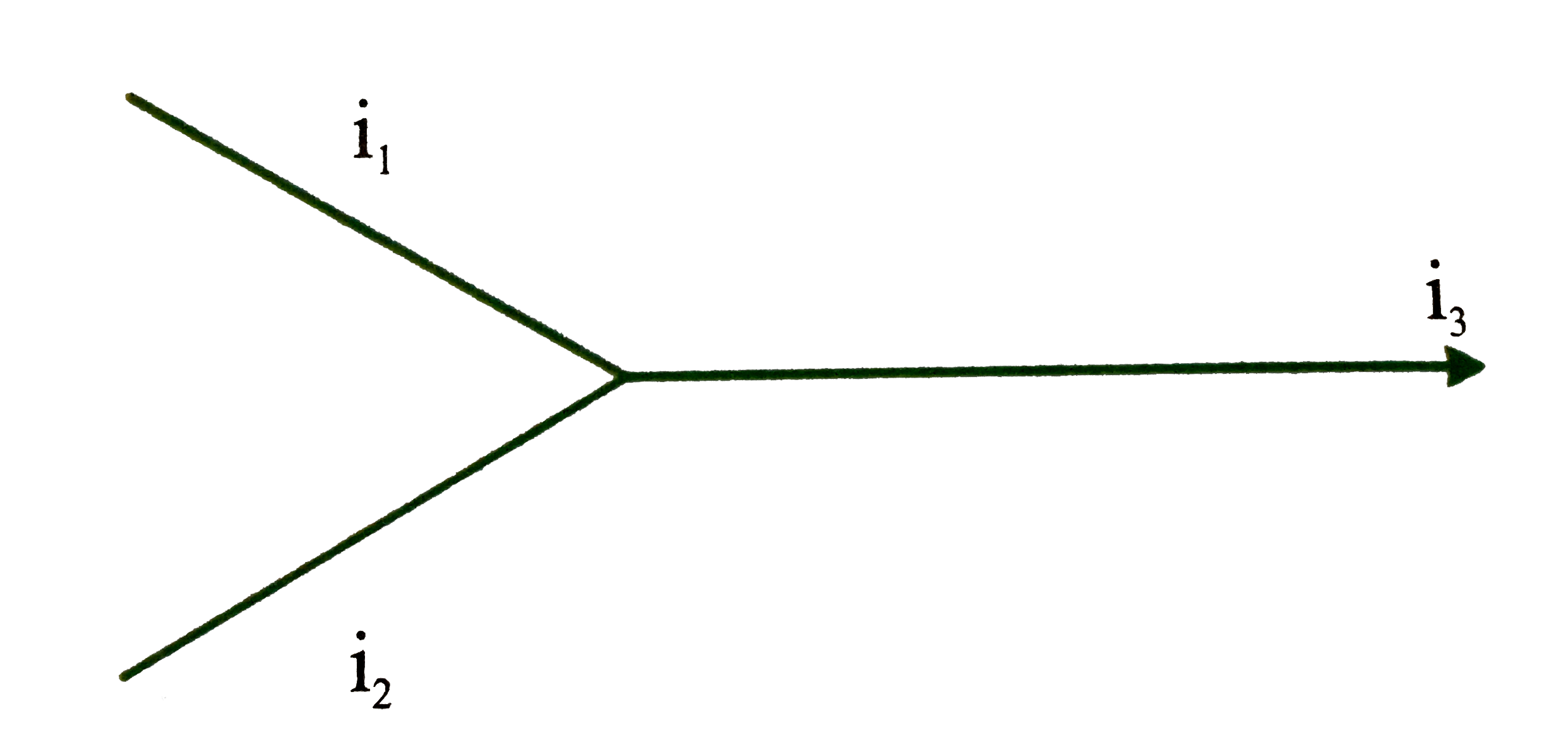A $\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2}} sin {ϕ + ω t}$
B $(i_{0_{1}} + i_{0_{2}}) sin (\frac{ϕ}{2} + ω t)$
C $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [ϕ + ω t]$
D $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [α + ω t]$ where $α = {Tan}^{- 1} [\frac{i_{0_{2}} sin ϕ}{i_{0_{1}} + i_{0_{2}} cos ϕ}]$

NTA MOCK TESTS-NTA NEET SET 115-PHYSICS

Home
Ask Doubt
Profile

Four sound sources produce the following four waves (i) y1=asin(ωt+ϕ1) (ii) y2=asin2ωt (iii) y3=a'sin(ωt+ϕ2) (iv) y4=a'sin(3ωt+ϕ) Superposition of which two waves gives rise to interference?

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check