Mayank, Mirza, Little and Jaspal bought a motorbike for Rs 60000. Mayank paid one-half of the sum of the amounts paid by the other boys, Mirza paid one-third of the sum of the amounts paid by the other boys and Little paid one-fourth of the sum of the amounts paid by the other boys. How much did Jaspal have to pay (a) Rs 13000 (b) Rs 15000 (c) Rs 17000 (d) None of these
To solve the problem step by step, we will denote the amounts paid by each person as follows:
- Let Mayank's payment be X
- Let Mirza's payment be Y
- Let Little's payment be Z
- Let Jaspal's payment be W
According to the problem, the total amount paid for the motorbike is Rs 60,000. Therefore, we have the equation:
1. Equation for total payment:
X+Y+Z+W=60000
Next, we will use the information given about how much each person paid in relation to the others.
2. Mayank's payment:
Mayank paid one-half of the sum of the amounts paid by the other boys:
X=12(Y+Z+W)
3. Mirza's payment:
Mirza paid one-third of the sum of the amounts paid by the other boys:
Y=13(X+Z+W)
4. Little's payment:
Little paid one-fourth of the sum of the amounts paid by the other boys:
Z=14(X+Y+W)
Now, we will substitute the expressions for Y and Z in terms of X and W into the total payment equation.
5. Substituting Mirza's payment:
From the equation for Mirza:
Y=13(X+Z+W)
Substitute Z:
Y=13(X+14(X+Y+W)+W)
6. Substituting Little's payment:
From the equation for Little:
Z=14(X+Y+W)
Substitute Y:
Z=14(X+13(X+Z+W)+W)
Now we can solve these equations step by step.
7. Solving for X:
From Mayank's equation:
X=12(Y+Z+W)
Substitute Y and Z into this equation and solve for X.
8. Finding values for Y and Z:
Similarly, use the equations for Y and Z to find their values.
9. Finding W:
Once you have X, Y, and Z, substitute these values back into the total payment equation to find W.
10. Final calculation:
After calculating W, you will find the amount Jaspal paid.
Final Calculation:
After solving the equations, we find:
- X=20000
- Y=15000
- Z=12000
- W=60000−(20000+15000+12000)=13000
Thus, Jaspal paid Rs 13,000.
- Let Mirza's payment be Y
- Let Little's payment be Z
- Let Jaspal's payment be W
X+Y+Z+W=60000
Mayank paid one-half of the sum of the amounts paid by the other boys:
X=12(Y+Z+W)
Mirza paid one-third of the sum of the amounts paid by the other boys:
Y=13(X+Z+W)
Little paid one-fourth of the sum of the amounts paid by the other boys:
Z=14(X+Y+W)
From the equation for Mirza:
Y=13(X+Z+W)
Substitute Z:
Y=13(X+14(X+Y+W)+W)
From the equation for Little:
Z=14(X+Y+W)
Substitute Y:
Z=14(X+13(X+Z+W)+W)
From Mayank's equation:
X=12(Y+Z+W)
Substitute Y and Z into this equation and solve for X.
Similarly, use the equations for Y and Z to find their values.
Once you have X, Y, and Z, substitute these values back into the total payment equation to find W.
After calculating W, you will find the amount Jaspal paid.
After solving the equations, we find:
- X=20000
- Y=15000
- Z=12000
- W=60000−(20000+15000+12000)=13000
Similar Questions
Knowledge Check
The amount collected by a trader to be paid to the government from the amount paid by him to the government is known as ……………..
AITCBGSTCOTCDITHow much a month are you paid ?
AHow much a month do you pay?BIn a month how much do you pay?CHow much a month do they pay you?DHow much a month do you pay them?A man borrows Rs. 4000 and pays back after 5 years at 15% simple interest. The amount paid by the man is :
ARs. 1800BRs. 4800CRs. 7500DRs. 7000
Deprecation is charged on the amount paid for the asset, including GST paid.
View SolutionShyama purchases a scooter costing Rs 36,450 and the rate of sales tax is 9%, then the total amount paid by her is
View Solution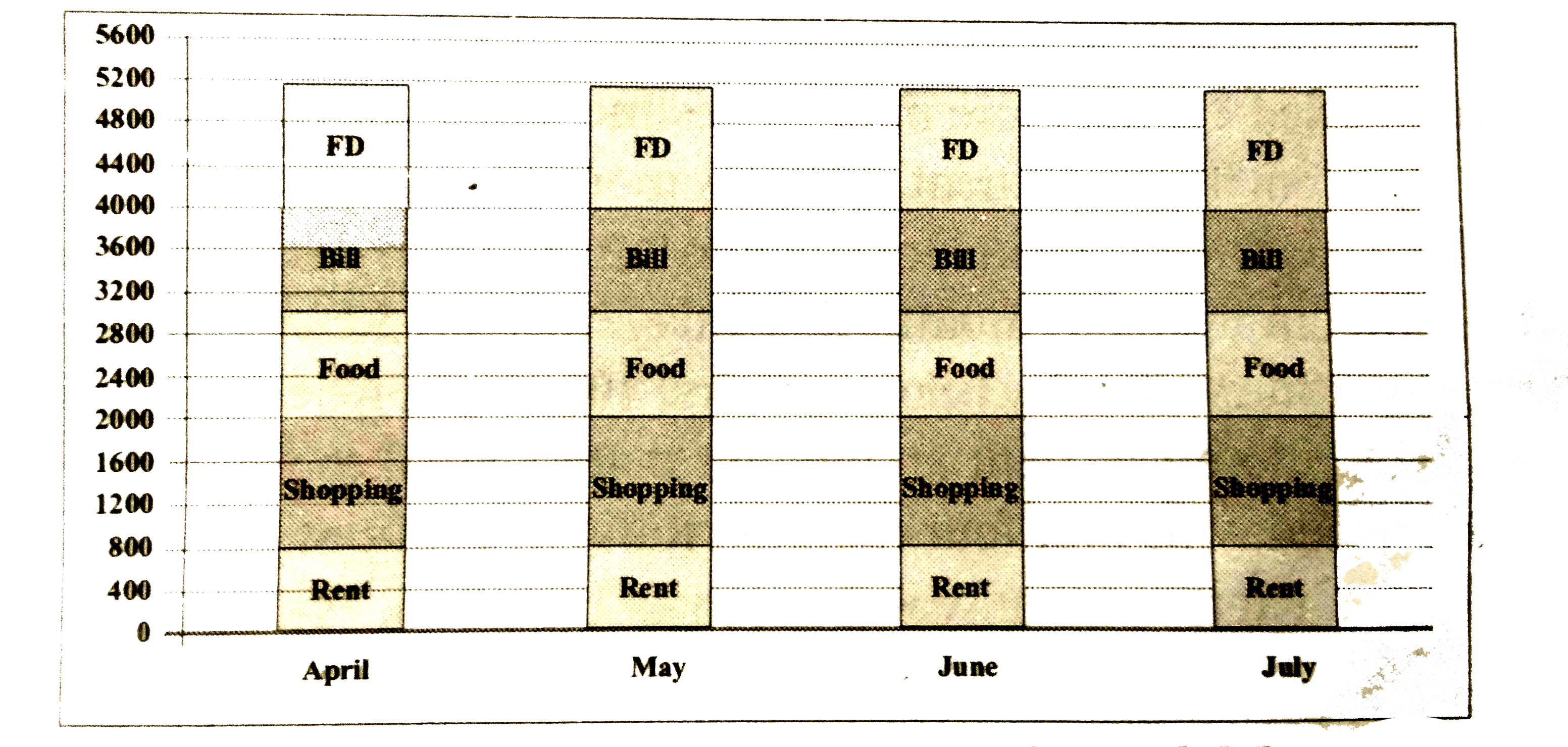
If amount padi by Abdul in month March on Rent is one fifth or rent paid by him in all months. Then find ratio of rent paid by him in March to amount paid by him on shopping in May ?
View SolutionIf 9 people go on a tour and pay a total of Rs 81,270.Find the amount paid by each person.
View Solution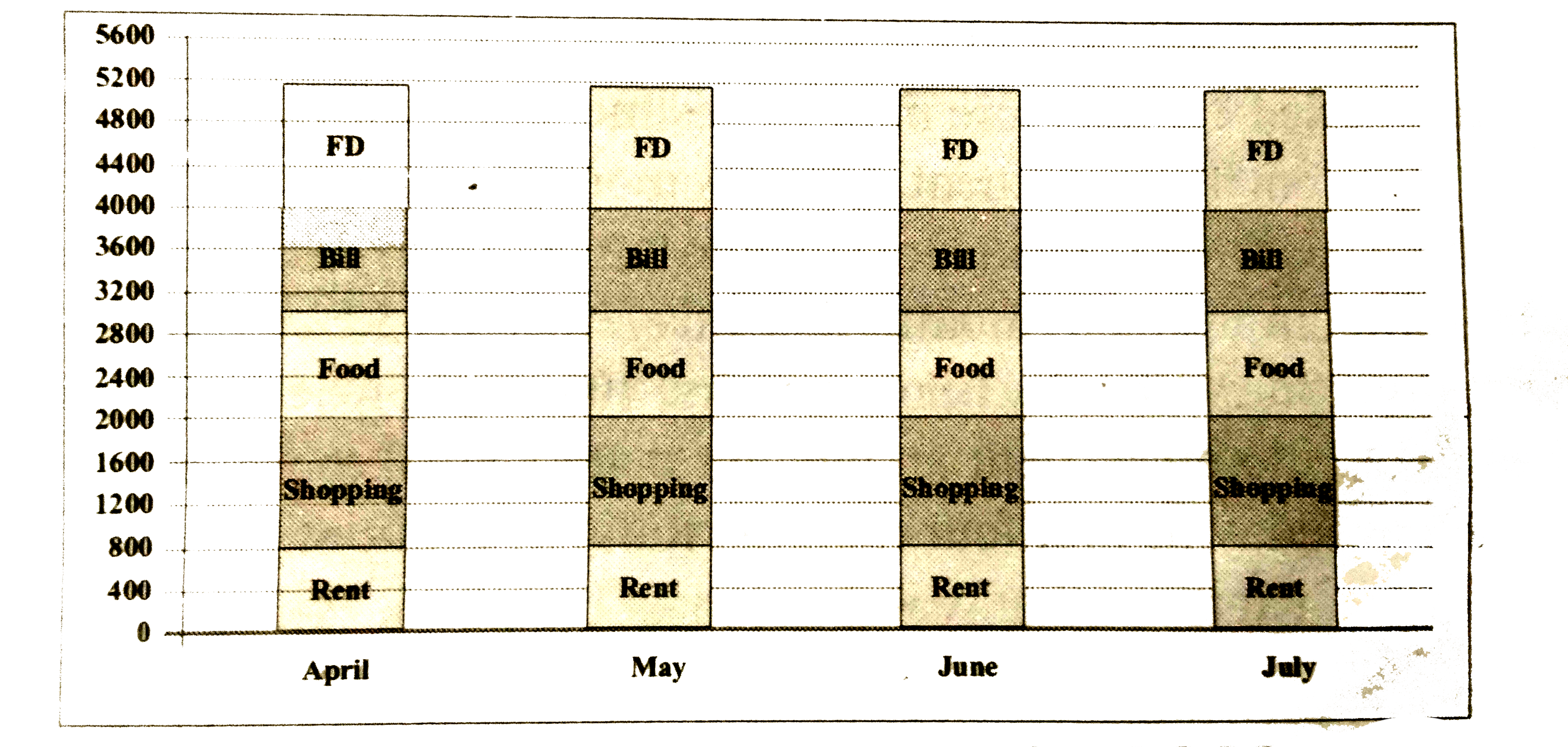
Average of amount paid by Abdul in FD, rent an food in mont May is what of average of amount paid by him on Shopping. Rent and Bill in month June ?
View Solution
