An area of 100 sq. cm on the map represents an area of 49 sq. km on the field. The R.F. of the scale to be used is 110000 (b) 120000 (c) 149000 (d) 170000
To find the representative fraction (R.F.) of the scale given that an area of 100 sq. cm on the map represents an area of 49 sq. km on the field, we can follow these steps:
Step 1: Understand the relationship between area on the map and area in reality
We know that:
- Area on the map = 100 sq. cm
- Area in reality = 49 sq. km
Step 2: Calculate the side lengths of the areas
Since we are dealing with areas, we can find the side lengths by taking the square root of both areas.
- Side length on the map = √(100 sq. cm) = 10 cm
- Side length in reality = √(49 sq. km) = 7 km
Step 3: Convert the real-world measurement to the same unit as the map
We need to convert 7 km into centimeters to compare it directly with the 10 cm on the map.
1 km = 1000 m = 100000 cm, so:
- 7 km = 7 × 100000 cm = 700000 cm
Step 4: Set up the R.F. formula
The representative fraction (R.F.) is given by the ratio of the length on the map to the length in reality:
R.F.=Length on mapLength in reality=10 cm700000 cm
Step 5: Simplify the R.F.
Now we simplify the fraction:
R.F.=10700000=170000
Conclusion
Thus, the R.F. of the scale to be used is:
(d) 170000
---
We know that:
- Area on the map = 100 sq. cm
- Area in reality = 49 sq. km
Since we are dealing with areas, we can find the side lengths by taking the square root of both areas.
- Side length in reality = √(49 sq. km) = 7 km
We need to convert 7 km into centimeters to compare it directly with the 10 cm on the map.
- 7 km = 7 × 100000 cm = 700000 cm
The representative fraction (R.F.) is given by the ratio of the length on the map to the length in reality:
R.F.=Length on mapLength in reality=10 cm700000 cm
Now we simplify the fraction:
R.F.=10700000=170000
Thus, the R.F. of the scale to be used is:
(d) 170000
Similar Questions
Knowledge Check
In the figure, side of each square is 1 cm. The area, in sq cm of the shaded part
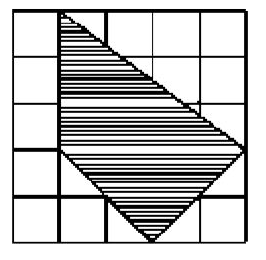 A8B9C10D11
A8B9C10D11In the figure, side of each square is 1 cm. The area, in sq cm of the shaded part
 A8B9C10D11
A8B9C10D11If the area of triangles is 100 sq. cm, r1=10 cm and r2=50 cm, then the value of (b−a) is equal to
A20B16C8D4
The area of a rectangular field is 52000 m2. This rectangular area has been drawn on a map to the scale 1 cm to 100 m. The length is shown as 3.25 cm on the map. The breadth of the rectangular field is (a) 150m (b) 160m (c) 200.5m (d) 300.5m
View SolutionIf the area of a triangle is 100sq,cm,r1=10cm and r2=50cm, then find the value of (b−a)
View SolutionThe readings in a field book are: (FIGURE) It is subsequently realised that the distances to C and D had been interchanged by mistake. The area of the actual field would be (a) 1300 sq. m (b) 1500 sq. m (c) 1800 sq. m (d) 2000 sq. m
View SolutionThe ratio of the areas of two squares is 1:4 .if the area of the first is 9 sq. units . The area of the first square is ____ ( in sq. units)
View SolutionThe radius of a circle is 1 cm less than half the side of a square whose area is 256 Sq.Cms. What is the area of the circle ?
View Solution
