क्षेत्र aB0 है, तथा क्षेत्र 2aB=−B0 है, जहाँ B, धनात्मक अचर है। वेग v=v0 जहाँ । धनात्मक अचर है, से चलता हुआ एक धनात्मक बिन्दु-आवेश चुम्बकीय क्षेत्र में x = a पर प्रवेश करता है। इस क्षेत्र में आवेश के पथ का सही निरूपण हो सकता है
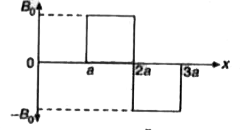
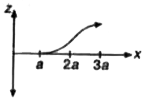
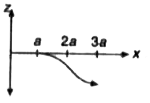
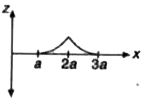
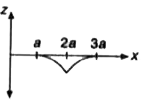
क्षेत्र altxlt2a के लिए,
F=q(v0ˆi)×B0ˆj=qv0B0ˆk
अत: पथ ऊपर की ओर को अवतल होगा। क्षेत्र 2 aF=q(v0ˆi)×(−B0ˆj)=−qv0B0ˆk
अतः पथ नीचे की ओर को अवतल होगा।
सही ग्राफ (6) है।
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - बहुविकल्पीय प्रश्न II11videos
चुम्बकत्व
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - सत्य/असत्य4videos
चुम्बकत्व
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - श्रृंखलाबद्ध बोधन प्रकार10videos
घूर्णन गति
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद III )2videos
तरंगे
Similar Questions
एक प्रोटॉन नियत वेग से चलता हुआ एक ऐसे स्थान में से होकर गुजरता है, जहाँ उसके वेग में कोई अन्तर नहीं पड़ता। यदिE व B क्रमश: वैद्युत तथा चुम्बकीय क्षेत्रों को प्रदर्शित करें तो इस स्थान में,
51:02View Solutionएकसमान चुम्बकीय क्षेत्र में मुक्त रूप से लटकायी गई आयताकार कुण्डली जिसमें एक स्थिर धारा बह रही है, उस पर कोई परिणामी बल कार्य नहीं करेगा।
34:22View Solutionदो डिस्कें A तथा B एक ऊर्ध्वाधर धुरी पर समाक्ष रूप से अवस्थिरत की गई है। उभयनिष्ठ अक्ष के परितः उन चकतियों के जड़त्व आघूर्ण क्रमशः I तथा 2I है। एक स्पि्रंग को x1 दूरी से दबाकर उसकी सम्पूर्ण स्थितिज ऊर्जा का उपयोग करके, चकती A को प्रारंभिक कोणीय वेग 2ω दिया जाता है। उतने ही स्पि्रंग गुणांक वाले एक दूसरे स्पि्रंग को x2 दूरी से दबाकर डिस्क B को कोणीय वेग ω दिया जाता है। दोनों चकतियां दक्षिणावर्त दिशा में घूम रही हैं
अनुपात x1/x2 है।41:18View Solutionअधिकतर पदार्थो का अपवर्तनांक, n>1 होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, sinθ1sinθ2=n2n1के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में εr व μr दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।58:30View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
01:19:21View Solutionचुम्बकीय क्षेत्र में आवेश की गति
50:12View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
45:12View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल | संयुक्त विद्युत चुम्बकीय क्षेत्र में आवेशित कण की गति
04:27View Solutionएकसमान चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव पर बल आधूर्ण तथा कार्य | पृथ्वी का चुम्बकीय क्षेत्र तथा अवयव | V,H तथा I में सम्बन्ध
45:31View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
45:46View Solutionएकसमान चुम्बकीय क्षेत्र में गतिमान आवेश (2)
01:31:26View SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। उपरोक्त प्रश्न में अक्ष से दूरी पर चुम्बकीय क्षेत्र जहाँ a lt x lt b है
01:23:21View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
01:33:02View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
47:45View Solutionएक समान चुम्बकीय क्षेत्र मे गतिमान आवेश
54:01View Solutionएक समान चुम्बकीय क्षेत्र मे गतिमान आवेश
51:30View Solution

