स्थिर आयतन एवं 300 K पर एक प्रथम कोटि की अभिक्रिया A(g)→2B(g)+C(g) के लिए, प्रारम्भ (t = 0) और समय t पर सम्पूर्ण दाब क्रमश: P0 और Pt हैं। शुरू में सिर्फ A,[A]0 सान्द्रता के साथ उपस्थित है, और A के आंशिक दाब को प्रारम्भिक मूल्य के 13 तक पहुंचने का समय t1/3 है। सही विकल्प है (है) (मान ले कि ये सारी गैसें आदर्श गैसों जैसा व्यवहार करती हैं)
दी गई अभिक्रिया के लिए (T=300K तथा स्थिर आयतन =V पर )
A(g)→2B9g)+C(g)
t=0 पर p0 − −
t=t पर p0−x 2x x
t=t1/3 पर [p0−2p03]=p03 4p03 2p03
हम गणना कर सकते हैं
pt=p0−x+2x+x=p0+2x
या 2x=pt−p0या x=pt−p02
अब प्रथम कोटि भी अभिक्रिया के लिए
t=1k In p0(p0−x)
x- का का मान समीकरण में रखने पर
t=1k In p0p0−(pt−p02)=1k In 2p02p0−pt+p0
या kt= In 2p0(3p0−pt) या kt= In 2p0− In (3p0−pt)
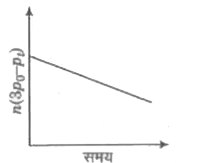
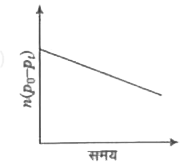
या In (3p0−pt)=−kt+In2p0
यह दर्शाता है कि (3p0−pt) तथा t के बीच ग्राफ ऋणात्मक ढाल के साथ सीधी रेखा के रूप में होगा।
अतः विकल्प a सही है।
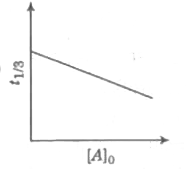
t1/3=1kInp0p0/3=1kIn3
यह दर्शाता है कि t1/3 प्रारंभिक सान्द्रता पर निर्भर नहीं होता है अतः विकल्प b गलत है।
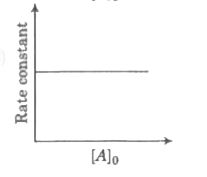
इसी प्रकार, दर स्थिरांक भी प्रांरभिक सान्द्रता पर निर्भरता नहीं दर्शाता है। अतः दर स्थिरांक तथा [A]0 के बीच ग्राफ X- अक्ष के समान्तर सीधी रेखा होगा।
Topper's Solved these Questions
- सॉल्वड पेपर्स 2018BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2018EXERCISE - पेपर II
18 Videos
- सॉल्वड पेपर 2017 JEE MAIN BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर 2017 JEE MAIN EXERCISE - MCQ
30 Videos
- सॉल्वड पेपर्स 2020BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2020EXERCISE - CHEMISTRY
36 Videos
Similar Questions
संकुल [Co(en)(NH3)3(H2O)]3+(en=H2NCH2CH2NH2) के विषय में सही विकल्प है (हैं)
View Solutionमोनोनाइट्रेशन अभिक्रिया में निम्न में से कौन-सा यौगिक मेटा उत्पाद की मह्त्वपूर्ण मात्रा उन्पन्न करेगा ?
View Solutionयदि किसी गैस के अणुओं की गतियों का वितरण नीचे दिये चित्र के अनुसार हो, तो अणुओं के अति-संभाव्य (प्रायिकतम, most probable,, औसत (average), तथा वर्ग माध्य मूल (root mean square) गतियों का अनुपात, क्रमशः है (चित्र में Fraction of molecules: अणुओं का अंश, तथा speed: गति),
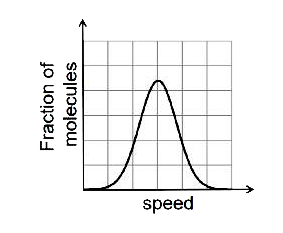
View Solution1 atm के बाह्य दाब के अंतर्गत गतिशील पिस्टन वाले एक निर्वातित पात्र में, He के 0.1 मोल और एक अज्ञात यौगिक के 1.0 मोल (0°C पर 0.68 atm वाष्प दाब) को रखा जाता है। आदर्श गैस व्यवहार मानते हुए, 0°C पर साम्यावस्था पर गैस का कुल आयतन (L में) लगभग x L के समान है। x के मान की गणना कीजिए।
View Solutionb = 0 और T = 300 K पर वॉन्डरवाल्स गैस के एक मोल के लिए PV और 7 के मध्य निम्न आरेख दर्शाया गया है। वॉन्डरवाल्स नियंताक a का मान (atm. "litre"^(2)" mol"^(-2) में) होगा
View Solutionएक द्रव, जल में अमिश्रणीय है जो कि 0.983 atm के दाब और 95.2^(@)C पर भाप आसवित है। आसुत में जल के प्रति ग्राम में उपस्थित द्रव का द्रव्यमान क्या है। द्रव का मोलर द्रव्यमान 134.3 g/mol है और जल का वाष्प दाब 0.84 atm है। साथ ही, शुद्ध द्रव का वाष्प दाब 0.143 atm है।
View Solutionदिया गया है कि n कोटि की अभिक्रिया के लिए दर समीकरण का समाकलित रूप k=1/(t(n-1))[1/(C^(n-1))-1/(C_0^(n-1))] है जहाँ C_0 और C प्रारंभ में और समय t के बाद अभिकारक सांद्रता के मान हैं। t_(3/4) और t_(1/2) के मध्य क्या संबंध है जहाँ t_(3/4) , C के ""^(1/4)C_0 होने के लिए आवश्यक समय है।
View Solutionनिम्नलिखित में से कोनसा आयतन (V ) और तापमान ( T ) ग्राफ एक वायुमंडलीय दाब पर एक आदर्श गैस के एक मोल के व्यवहार को दर्शाता है
View Solution298K पर, शुद्ध द्रवों A और B के वाष्प दाब क्रमशः 400 और 600 mm Hg है। दो द्रवों को मिलाने पर, उनके प्रारंभिक आयतन का योग अंतिम मिश्रण के आयतन के बराबर होता हैं मिश्रण में द्रव B का मोल प्रभाज 0.5 हे। अंतिम विलयन का वाष्प दाब, वाष्प प्रावस्था में घटकों A और B के मोल प्रभाज क्रमशः है:
View Solution1 atm के बाह्य दाब पर He के 0.1 मोल और अज्ञात यौगिक ( 0^(@)C पर वाष्प दाब 0.68 atm है। )के 1.0 मोल को गतिशील पिस्टन वाले एक निर्वातित पात्र में लिया गया है। आदर्श गैस के व्यवहार पर विचार करते हुए 0^(@)C पर गैसों का कुल आयतन (लीटर में) लगभग है
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solutionडाइमेथिल ईथर के अपघटन के फलस्वरूप CH_4, H_2 " और " CO का निर्माण होता है और अभिक्रिया दर = k[CH_3OCH_3]^(3/2) द्वारा दर्शायी जाती है। अभिक्रिया की दर, बंद पात्र में दाब में वृद्धि का अनुगमन करती है, इसलिए डाइमेथिल ईथर के आंशिक दाब के संदर्भ में भी दर को व्यक्त किया जा सकता है, अर्थात दर = k(PCH_3 OCH_3 )^(3/2) यदि दाब को बार तथा समय को मिनटों में मापा जाए, तब दर स्थिरांक की इकाई क्या होगी?
View Solutionअभिक्रिया A(g) to B(g)+2C(g) , दर स्थिरांक 2.303 xx 10^(-3)s^(-1) के साथ एक प्रथम-कोटि की अभिक्रिया है। 300 K और नियत दाब पर एक 2 लीटर के पात्र में 'A' के 0.1 मोल के साथ अभिक्रिया प्रारंभ करने पर 301 सेकंड के बाद A की सांद्रता ज्ञात कीजिए।
View Solutionअभिक्रिया A (g)=B(g)iff C(g) के लिए Kc और Kp के बीच संबंध है:
View Solutionशून्य कोटि अभिक्रिया के लिए, सांद्रता और समय के बीच का आरेख निम्न के साथ रेखीय होता है:
View Solution
