Find the magnetic field at the centre O of the loop shown in the figure.

Video Solution
Text Solution
Due to straight parts, there is no magnetic field at O. There are three fields at O.
B1=μ0i4π(4R)×π2 (∴B=μ0i4πRθ), Due to arc of radius 4R
B2=μ0i4π(2R)(π), due to arc of radius 2R
As the currenct is anticlockwise in all three arcs, therefore, all the fields are perpendicular to plane and outwards.
⇒Bnet=B1+B2+B3
∴Bnet=μ0iR[132+18+18]=9μ0i32R
|
Topper's Solved these Questions
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - ILLUSTRATION
12 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - TRY YOURSELF
11 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
Similar Questions
Knowledge Check
The magnetic field at the centre O of the are shown in the figure is
 A2I(√2+π)×10−7rB2I(√2+π4)×10−7rCI(√2+π)×10−7rDI(√2+π4)×10−7r
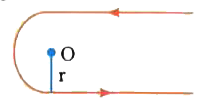
A2I(√2+π)×10−7rB2I(√2+π4)×10−7rCI(√2+π)×10−7rDI(√2+π4)×10−7rThe magnetic field at the centre of semicircle o in the figure is
 AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)The magnetic field at the centre of semicircle o in the figure is
 AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
The wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.

View SolutionFind the magnetic field at the centre P of square of side a shown in
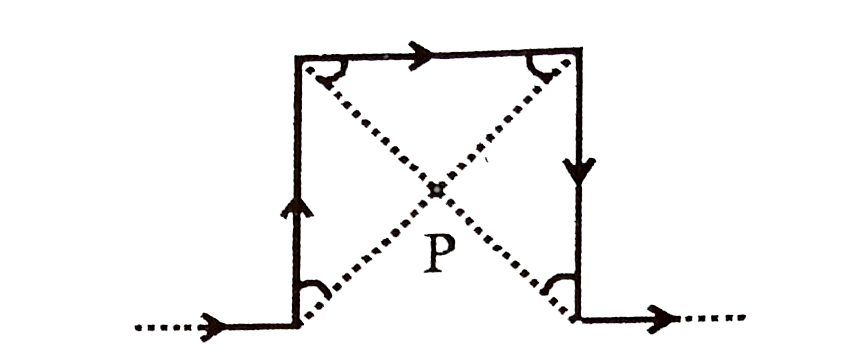 .
.
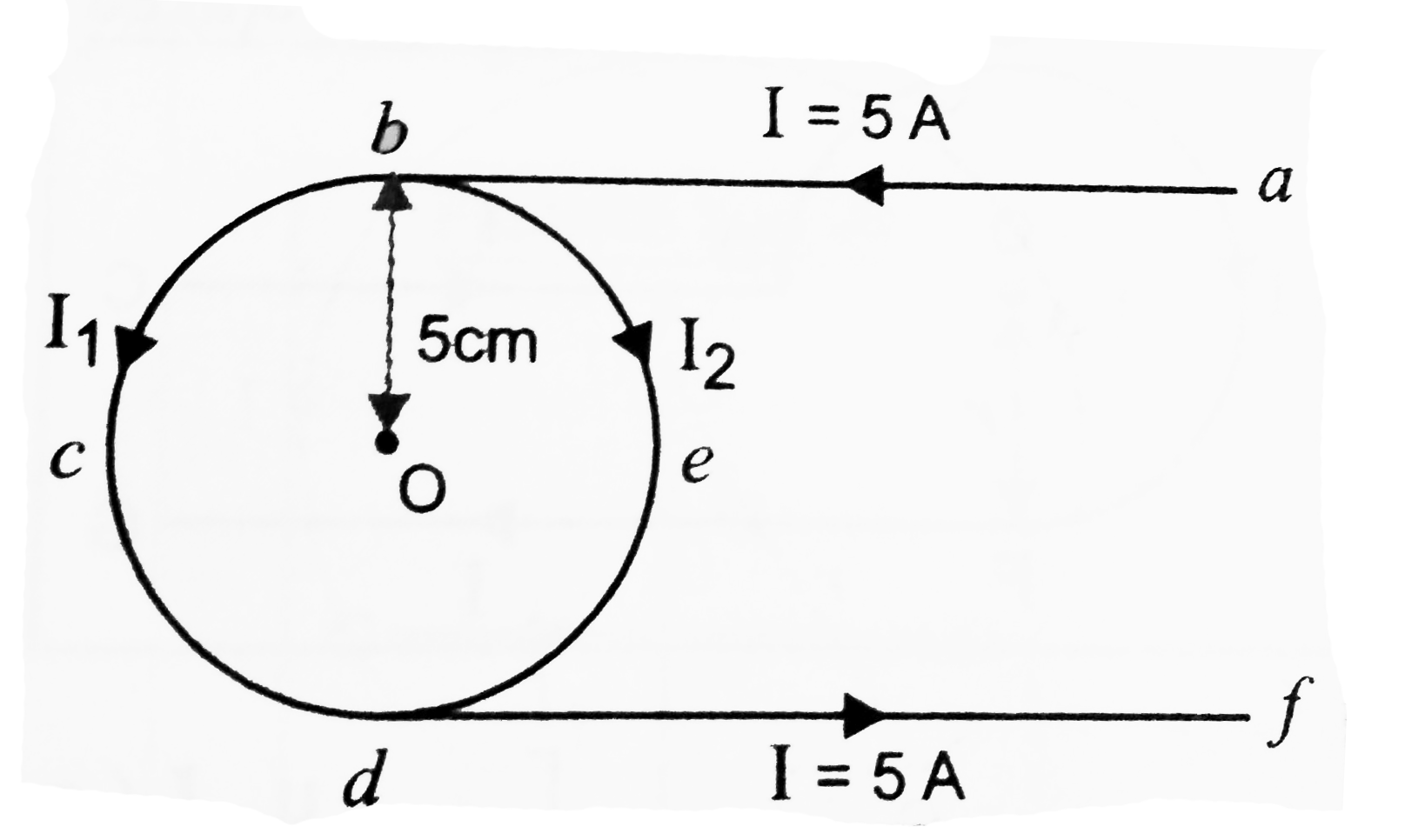
View SolutionIn the net work shown in figure,find the magnetic field at the centre O of the coil.
View SolutionA square loop of side length L carries a current which produces a magnetic field B0 at the centre (O) of the loop. Now the square loop is folded into two parts with one half being perpendicular to the other (see fig). Calculate the magnitude of magnetic field at the centre O.

View SolutionThe magnetic field at the centre the figure is
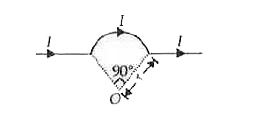
View Solution


