The figure shows the top view of a conducting rod AB bent to form a semicircle of radius R, carrying current I, placed on a smooth horizontal table. It is subjected to uniform magnetic field B perpendicular to its plane as shown. The rod is held at rest in it position by two light strings attached to its ends. Calculate the tension in the strings.

Tension in the strings balances the magnetic force acting on the rod AB.
Magnetic force on AB is Bi× (effective length )=Bi2R
Thus 2T=Bi2R
T=BiR
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - ILLUSTRATION12videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - TRY YOURSELF11videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)2videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)5videos
MOVING CHARGES AND MAGNETISM
Similar Questions
The figure shows top view of a conducting rob AB, bent to form a semicircle of radius R, carrying current I, placed on a smooth horizontal table. It is subjected to a uniform magnetic field B perpendicular to its plane as shown. The rod is held at rest in its position by two light strings attached to its ends. Calculate the magnetic force acting on the conductor AB and the tension in the strings.
Strategy: To find the force conductor, consider a small arc of length dl=Rdθ. This arc can be consider as a straight conductor of length dl.View SolutionA rectangular coil of sides l and b carrying a current I is subjected to a uniform magnetic field →B acting perpendicular to its plane. Obtain the expression for the torque on it.
View Solution
Knowledge Check
- Question 1 - Select One
A conducting ring of radius 2R rolls on a smooth horizontal conducting surface as shown in figure-5.295. A uniform horizontal magnetic field B is perpendicular to the plane of the ring. The potential of A with respect to O is:
 A2 BvRB12BvRC8BvRD4BvR
A2 BvRB12BvRC8BvRD4BvR - Question 2 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
AzeroBir BC2π ir BDπirB - Question 3 - Select One
A conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
AI r BB2πrIBCzeroDπrIB
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
View SolutionA conducting rod AB is bent in the form of a semicircle of radius R. It is kept in a region of uniform magnetic field B such that plane of semicircle is perpendicular to magnetic field. This rod is being moved with a constant speed v perpendicular to AB. Find the emf developed between the ends.
View SolutionA conducting wire bent in the form of a parabola y2=2x, carries a current I=2A as shown in figure. The wire is subjected to a uniform magnetic field →B=−2ˆk tesla. The magnetic force on the wire in (newton) is
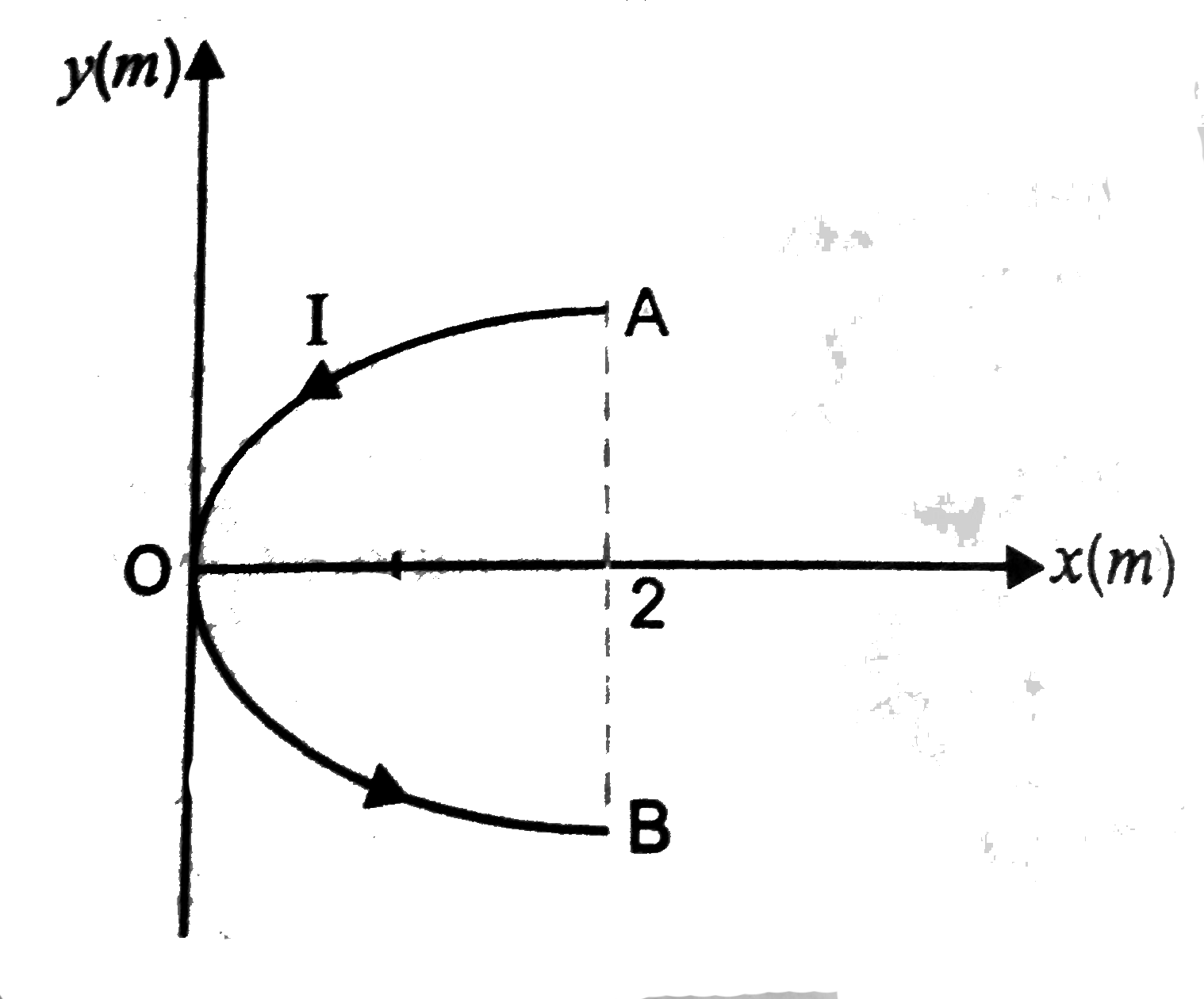 View Solution
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View Solution
