If a charged particle enters perpendicular in the uniform magnetic field then
Energy remains constant but moment changes
Energy and momentum both remains constant
Momentum remains constant but energy changes
Neither energy nor momentum remains constant
The correct Answer is:A
To solve the question regarding the behavior of a charged particle entering a uniform magnetic field perpendicularly, we can break down the solution step by step.
1. Understanding the Situation:
- A charged particle (like an electron or proton) is entering a uniform magnetic field at a right angle (90 degrees) to the direction of the magnetic field lines.
2. Magnetic Force on the Charged Particle:
- The magnetic force acting on a charged particle moving in a magnetic field is given by the Lorentz force equation:
→F=q(→v×→B)
where q is the charge of the particle, →v is the velocity vector of the particle, and →B is the magnetic field vector.
3. Direction of the Force:
- Since the particle enters the magnetic field perpendicularly, the angle between the velocity vector and the magnetic field vector is 90 degrees. Thus, the magnetic force will be at a right angle to the velocity of the particle.
4. Work Done by the Magnetic Field:
- The work done by a force is given by the equation:
W=→F⋅→d
where →d is the displacement. Since the magnetic force is always perpendicular to the displacement of the charged particle, the work done by the magnetic field is zero:
W=0
5. Kinetic Energy:
- Since the work done is zero, the kinetic energy of the charged particle remains constant. The equation for kinetic energy is:
KE=12mv2
where m is the mass and v is the speed of the particle. Since the speed does not change, the kinetic energy remains constant.
6. Momentum Change:
- Although the kinetic energy remains constant, the direction of the velocity changes due to the magnetic force acting on the particle. Momentum →p is given by:
→p=m→v
Since the direction of →v changes, the momentum of the particle also changes even though its magnitude (speed) remains constant.
7. Conclusion:
- Therefore, when a charged particle enters a uniform magnetic field perpendicularly, the energy remains constant while the momentum changes due to the change in direction of the velocity.
Final Answer:
- Energy remains constant, but momentum changes.
- A charged particle (like an electron or proton) is entering a uniform magnetic field at a right angle (90 degrees) to the direction of the magnetic field lines.
- The magnetic force acting on a charged particle moving in a magnetic field is given by the Lorentz force equation:
→F=q(→v×→B)
where q is the charge of the particle, →v is the velocity vector of the particle, and →B is the magnetic field vector.
- Since the particle enters the magnetic field perpendicularly, the angle between the velocity vector and the magnetic field vector is 90 degrees. Thus, the magnetic force will be at a right angle to the velocity of the particle.
- The work done by a force is given by the equation:
W=→F⋅→d
where →d is the displacement. Since the magnetic force is always perpendicular to the displacement of the charged particle, the work done by the magnetic field is zero:
W=0
- Since the work done is zero, the kinetic energy of the charged particle remains constant. The equation for kinetic energy is:
KE=12mv2
where m is the mass and v is the speed of the particle. Since the speed does not change, the kinetic energy remains constant.
- Although the kinetic energy remains constant, the direction of the velocity changes due to the magnetic force acting on the particle. Momentum →p is given by:
→p=m→v
Since the direction of →v changes, the momentum of the particle also changes even though its magnitude (speed) remains constant.
- Therefore, when a charged particle enters a uniform magnetic field perpendicularly, the energy remains constant while the momentum changes due to the change in direction of the velocity.
- Energy remains constant, but momentum changes.
Topper's Solved these Questions
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION B
25 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION C
48 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - EXERCISE
30 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
Similar Questions
Knowledge Check
A charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. The angle of deviation θ time taken by particle to cross magnetic field will be
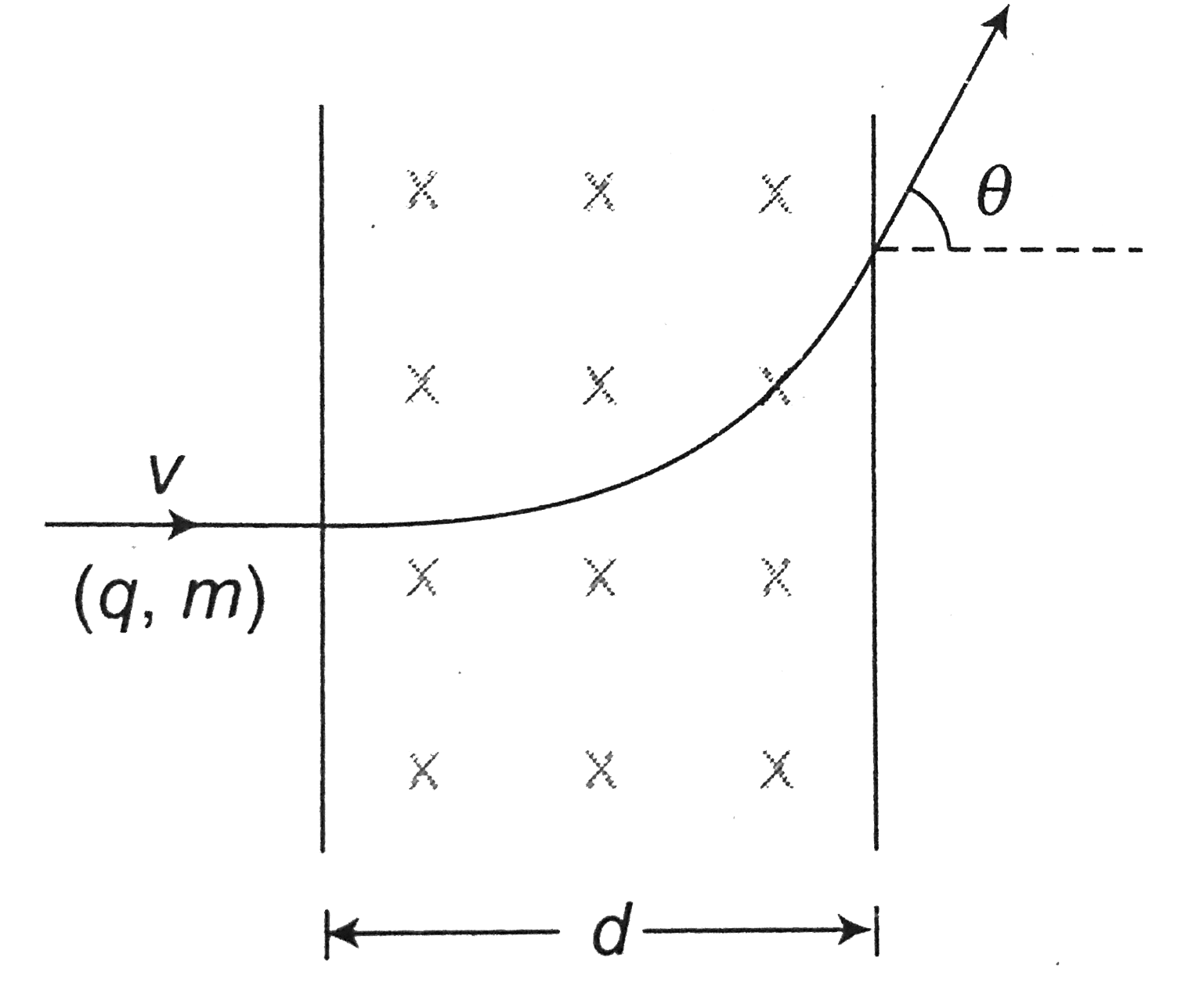 Asin−1.Bqdmv,mθBqBsin−1.Bqvmd,mθBqCcos−1.Bqdmv,mθBqDcos−1.Bqvmd,mθBq
Asin−1.Bqdmv,mθBqBsin−1.Bqvmd,mθBqCcos−1.Bqdmv,mθBqDcos−1.Bqvmd,mθBqAssertion When a charged particle moves perpendicular to a uniform magnetic field then its momentum remains constant.
Reason Magnetic force acts perpendicular to the velocity of the particle.AIf both Assertion and Reason are true and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are true but Reason is not correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.If a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
AT2∝r3BT2∝rCT∝r2DT∝r0
Assertion If a charged particle enters from outside in uniform magnetic field, then it will keep on rotating in a circular path.
Reson Magnetic force is always perpendicular to velocity vector.
View SolutionWhen a charged particle moves perpendicular to a magnetic field, then:
View SolutionWhen a charged particle moves perpendicular to a magnetic field, then:
View SolutionThe path executed by a charged particle, whose motion is perpendicular to a uniform megnetic field, is
View SolutionThe path executed by a charged particle whose motion is perpendicular to magnetic field is
View Solution
