In a toroid the number of tuns per unit length is 1000 and current through it is ampere. The magnetic field produced inside (in ) will be
The correct Answer is:C
To find the magnetic field produced inside a toroid, we can use Ampere's circuital law. The formula for the magnetic field B inside a toroid is given by:
B=μ0NI2πr
Where:
- B is the magnetic field inside the toroid,
- μ0 is the permeability of free space, approximately 4π×10−7T m/A,
- N is the total number of turns,
- I is the current flowing through the wire,
- r is the radius of the toroid.
However, in this case, we are given the number of turns per unit length n and the current I.
1. Identify the given values:
- Number of turns per unit length n=1000turns/m
- Current I=14πA
2. Calculate the total number of turns N:
Since we are not given the radius, we can express the magnetic field in terms of n:
N=n⋅L
where L is the length of the toroid. We can use n directly in the formula.
3. Substituting into the formula:
The formula for the magnetic field inside the toroid can be simplified using n:
B=μ0nI
4. Substituting the values:
B=(4π×10−7)×(1000)×(14π)
5. Simplifying the expression:
B=(4π×10−7)×1000×14π=10−4T
6. Convert to Weber/m²:
Since 1T=1Wb/m2, we have:
B=10−4Wb/m2
Thus, the magnetic field produced inside the toroid is 10−4Wb/m2.
- B is the magnetic field inside the toroid,
- μ0 is the permeability of free space, approximately 4π×10−7T m/A,
- N is the total number of turns,
- I is the current flowing through the wire,
- r is the radius of the toroid.
- Number of turns per unit length n=1000turns/m
- Current I=14πA
Since we are not given the radius, we can express the magnetic field in terms of n:
N=n⋅L
where L is the length of the toroid. We can use n directly in the formula.
The formula for the magnetic field inside the toroid can be simplified using n:
B=μ0nI
B=(4π×10−7)×(1000)×(14π)
B=(4π×10−7)×1000×14π=10−4T
Since 1T=1Wb/m2, we have:
B=10−4Wb/m2
Topper's Solved these Questions
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION B
25 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION C
48 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - EXERCISE
30 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
Similar Questions
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionA solenoid is a long helical coil of wire through which a current is run in order to create a magnetic field. The magnetic field of the solenoid is the superposition of the fields due to the current through each coil. It is nearly uniform inside the solenoid and close to zero outside and is similar to the field of a bar magnet having a north pole at one end and a south pole at the other depending upon the direction of current flow. The magnetic field produced in the solenoid is dependent on a few factors such as, the current in the coil, number of turns per unit length etc. The following graph is obtained by a researcher while doing an experiment to see the variation of the magnetic field with respect to the current in the solenoid. The unit of magnetic field as given in the graph attached is in milli-Tesla (mT) and the current is given in Ampere.
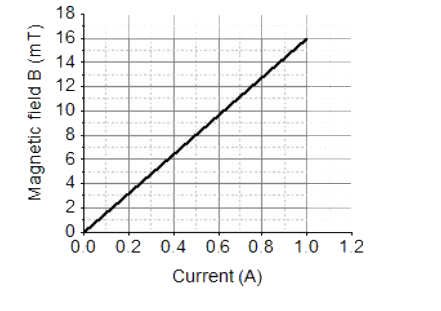
The magnetic field lines produced inside the solenoid are similar to that of …
View Solution
Knowledge Check
A toroid has number of turns per unit length n, current i, then the magnetic field is
Aμ0niBμ0n2iCμ0i/nDNone of theseAn air core toroid with 10 turns/cm carries a current of 1 milliampere. The intensity of magnetic field inside it, in weber/m2 will be-
A4π×10−6B4π×10−7C4π×10−8D4π×10−9Two coaxil solenoids 1 and 2 of the same length are set so that one is inside the other. The number of turns per unit length are n1 and n2. The current i1 and i2 are flowing in opposite directions. The magnetic field inside the inner coil is zero. This is possible when
Ai_(2)cancel(=)i_(2) and n1=n2Bi2=i2 and n_(1)cancel(=)n_(2)Ci2=i2 and n1=n2Di1n1=i2n2
A solenoid is a long helical coil of wire through which a current is runs in order to create a magnetic field. The magnetic field of the solenoid is the superposition of the fields due to the current through each coil. It is nearly uniform inside the solenoid and close to zero outside and is similar to the field of a bar magnet having a north pole at one end and a south pole at the other depending upon the direction of current flow. The magnetic field produced in the solenoid is dependent on a few factors such as, the current in the coil, number of turns per unit length etc.
The following graph is obtained by a researcher while doing an experiment to see the variation of the magnetic field with respect to the current in the solenoid.
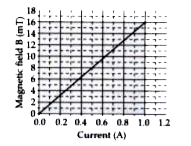
The unit of magnetic field as given in the graph attached is in milli-Tesla (mT) and the current is given in Ampere.
The magnetic field lines produced inside the solenoid are similar to that of ............
View SolutionMean radius of a toroid is 10 cm and number of turns is 500. If current flowing through it is 0.1 A then value of magnetic induction (in tesla) for toroid is
View SolutionA long solenoid has 200 turns per cm and carries a current of 2.5 amps. The magnetic field at its centre is (μ0=4π×10−7weber/amp−m)
View SolutionA wire is wound on a long rod of material of relative permeability μr=4000 to make a solenoid.If the current through the wire is 5A and number of turns per unit length is 1000 per metre,then the magnetic field inside the solenoid is:
View SolutionA wire is wound on a long rod of material of relative permeability μr=4000 to make a solenoid. If the current through the wire is 5 A and number of turns per unit length is 1000 per metre, then the magnetic field inside the solenoid is
View Solution
