A particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
To solve the problem of finding the final velocity of two identical particles colliding perfectly inelastically, we can follow these steps:
Step 1: Understand the Initial Conditions
We have two particles, each with mass m:
- Particle 1 is moving in the positive x-direction with speed v.
- Particle 2 is moving in the positive y-direction with speed v.
Step 2: Write the Initial Momentum
The momentum of each particle can be expressed as:
- Momentum of Particle 1:
→p1=m⋅v^i
- Momentum of Particle 2:
→p2=m⋅v^j
Step 3: Calculate Total Initial Momentum
The total initial momentum →pinitial of the system is the vector sum of the momenta of both particles:
→pinitial=→p1+→p2=m⋅v^i+m⋅v^j
This can be simplified to:
→pinitial=mv(^i+^j)
Step 4: Apply Conservation of Momentum
Since the collision is perfectly inelastic, the two particles stick together after the collision. The total mass after the collision is 2m. Let →vf be the final velocity of the combined mass. According to the conservation of momentum:
→pinitial=→pfinal
Thus,
mv(^i+^j)=(2m)→vf
Step 5: Solve for Final Velocity
We can cancel m from both sides (assuming m≠0):
v(^i+^j)=2→vf
Now, divide both sides by 2:
→vf=v2(^i+^j)
Step 6: Find the Magnitude of Final Velocity
To find the magnitude of →vf:
|→vf|=∣∣∣v2(^i+^j)∣∣∣=v2√12+12=v2√2=v√22
Step 7: Determine the Direction of Final Velocity
The direction of →vf can be found using the angle θ:
tanθ=vyvx=v/2v/2=1⟹θ=45∘
Final Result
The final velocity of the combination is:
→vf=v2(^i+^j)with magnitudev√22and direction45∘
---
We have two particles, each with mass m:
- Particle 1 is moving in the positive x-direction with speed v.
- Particle 2 is moving in the positive y-direction with speed v.
The momentum of each particle can be expressed as:
- Momentum of Particle 1:
→p1=m⋅v^i
- Momentum of Particle 2:
→p2=m⋅v^j
The total initial momentum →pinitial of the system is the vector sum of the momenta of both particles:
→pinitial=→p1+→p2=m⋅v^i+m⋅v^j
This can be simplified to:
→pinitial=mv(^i+^j)
Since the collision is perfectly inelastic, the two particles stick together after the collision. The total mass after the collision is 2m. Let →vf be the final velocity of the combined mass. According to the conservation of momentum:
→pinitial=→pfinal
Thus,
mv(^i+^j)=(2m)→vf
We can cancel m from both sides (assuming m≠0):
v(^i+^j)=2→vf
Now, divide both sides by 2:
→vf=v2(^i+^j)
To find the magnitude of →vf:
|→vf|=∣∣∣v2(^i+^j)∣∣∣=v2√12+12=v2√2=v√22
The direction of →vf can be found using the angle θ:
tanθ=vyvx=v/2v/2=1⟹θ=45∘
The final velocity of the combination is:
→vf=v2(^i+^j)with magnitudev√22and direction45∘
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION2videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF95videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively perpendicular to each other collides perfectly inelastically, then
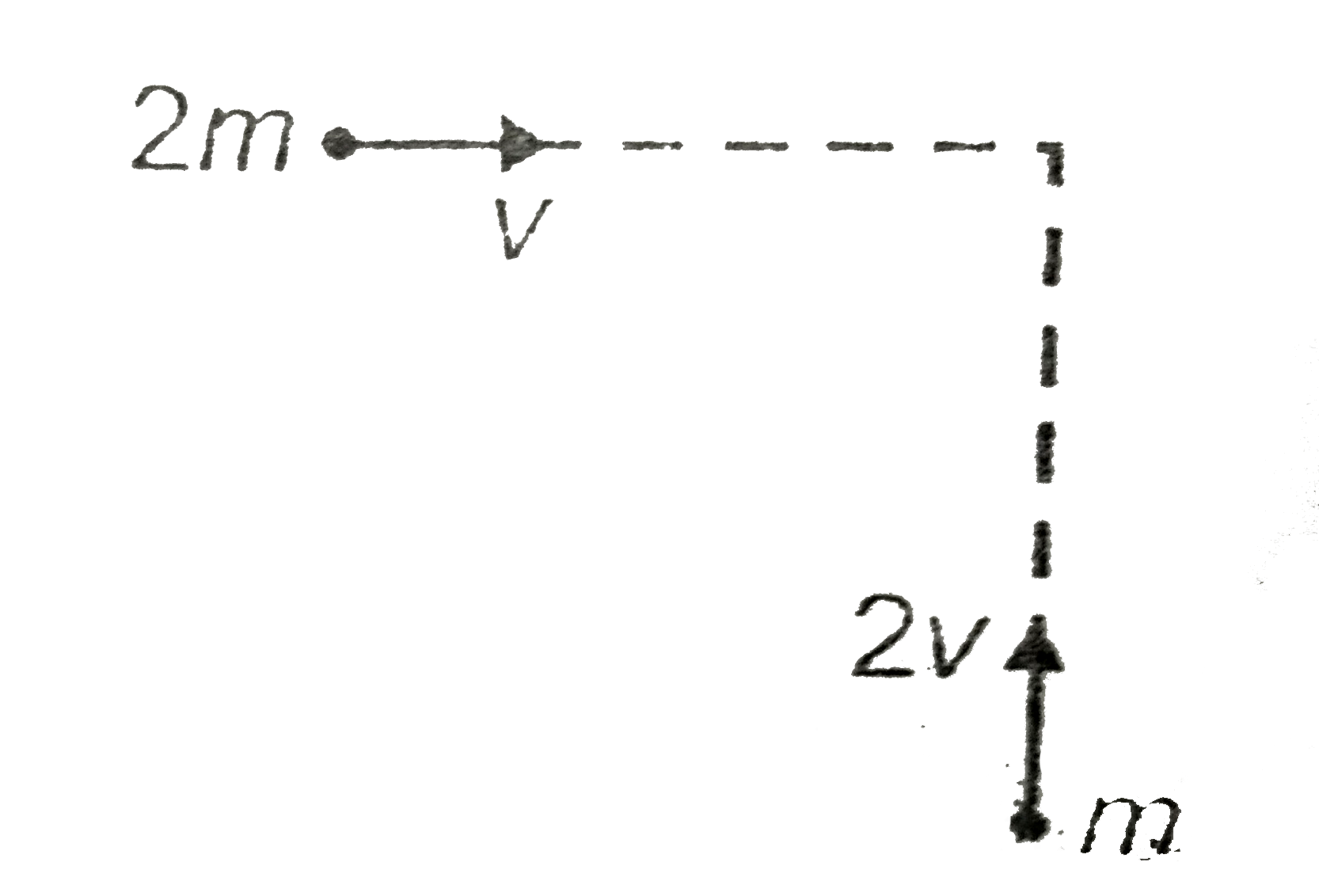
Loss in kinetic energy of the systemView Solution
Knowledge Check
- Question 1 - Select One
A ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
Aboth the balls come to restBthe velocities are exchanged between the two ballsCboth of them move at right angles to the original line of motionDone ball comes to rest and another ball travels back with velocity 2v - Question 2 - Select One
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
A34μ2B38μ2C14μ2D18μ2 - Question 3 - Select One
A particle of mass m1 moving with velocity v in a positive direction collides elastically with a mass m2 moving in opposite direction also at velocity v. If m2>>m1, then
Athe velocity of m1 immediately after collision is nearly 3vBthe change in momentum of m1 is nearly 4m1vCthe change in kinetic energy of m1 is nearly 4mv2Dall of the above
Two particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collisionView SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
View SolutionTwo particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
View SolutionTwo identical mass M moving with velocity u1andu2 collide perfectly inelastically. The loss in kinetic energy is
View Solution

