A particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
U(x)>E
E(x)<E
U(x)=0
U(x)≤E
The correct Answer is:D
To solve the problem, we need to analyze the motion of a particle with total energy E in a potential energy region U(x). The key concept here is that the total energy of the particle is the sum of its kinetic energy and potential energy.
1. Understanding Total Energy:
The total energy E of the particle is given by the equation:
E=K+U(x)
where K is the kinetic energy and U(x) is the potential energy at position x.
2. Expressing Kinetic Energy:
Rearranging the equation gives us:
K=E−U(x)
This equation tells us that the kinetic energy K is equal to the total energy E minus the potential energy U(x).
3. Condition for Motion:
Kinetic energy must always be non-negative, as it cannot be less than zero:
K≥0
Substituting the expression for kinetic energy, we have:
E−U(x)≥0
4. Rearranging the Inequality:
From the inequality E−U(x)≥0, we can rearrange it to find:
E≥U(x)
5. Conclusion:
This means that the motion of the particle is restricted to the region where the total energy E is greater than or equal to the potential energy U(x). Therefore, the particle can only exist in regions where its total energy is greater than or equal to the potential energy at that point.
Final Answer:
The motion of the particle is restricted to the region where:
E≥U(x)
The total energy E of the particle is given by the equation:
E=K+U(x)
where K is the kinetic energy and U(x) is the potential energy at position x.
Rearranging the equation gives us:
K=E−U(x)
This equation tells us that the kinetic energy K is equal to the total energy E minus the potential energy U(x).
Kinetic energy must always be non-negative, as it cannot be less than zero:
K≥0
Substituting the expression for kinetic energy, we have:
E−U(x)≥0
From the inequality E−U(x)≥0, we can rearrange it to find:
E≥U(x)
This means that the motion of the particle is restricted to the region where the total energy E is greater than or equal to the potential energy U(x). Therefore, the particle can only exist in regions where its total energy is greater than or equal to the potential energy at that point.
The motion of the particle is restricted to the region where:
E≥U(x)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
15 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
39 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle is moving in a potential region defined by U=K(x2+y2+z2). Calculate the force acting on the particle.
View SolutionKinetic energy of a particle on the surface of earth is E0 and the potential energy is −2E0.
(a) Will the particle escape to infinity ?
(ii) What is the value of potential energy where speed of the particle becomes zero?
View Solution
Knowledge Check
A particle with total energy E moves in one dimemsional region where the potential energy is U(x) The speed of the particle is zero where
AU(x)=0BU(x)=ECdU(x)dx=0Dd2U(x)dx2=0A particle with total energy E moves in one direction in a region where, the potential energy is U The acceleration of the particle is zero, where,
AU=EBU=0CdUdx=0Dd2Udx2=0A particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
A2π√mk+4√2Emg2B2π√mkCπ√mk+2√2Emg2D2√2Emg2
Kinetic energy of a particle on the surface is e0 and potential energy is−E02.
(a) Will the particle escape to infinity ?
(b) At some height some height its kinetic energy becomes 0.6E0. What is potential energy at this height ?
(c) If the particle escape to infinity , what is kinetic energy of the particle at infinity ?
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
View SolutionA potential energy curve U(x) is shown in the figure. What value must the mechanical energy Emec of the particle not exceed, if the particle is to be trapped within the region shown in graph?
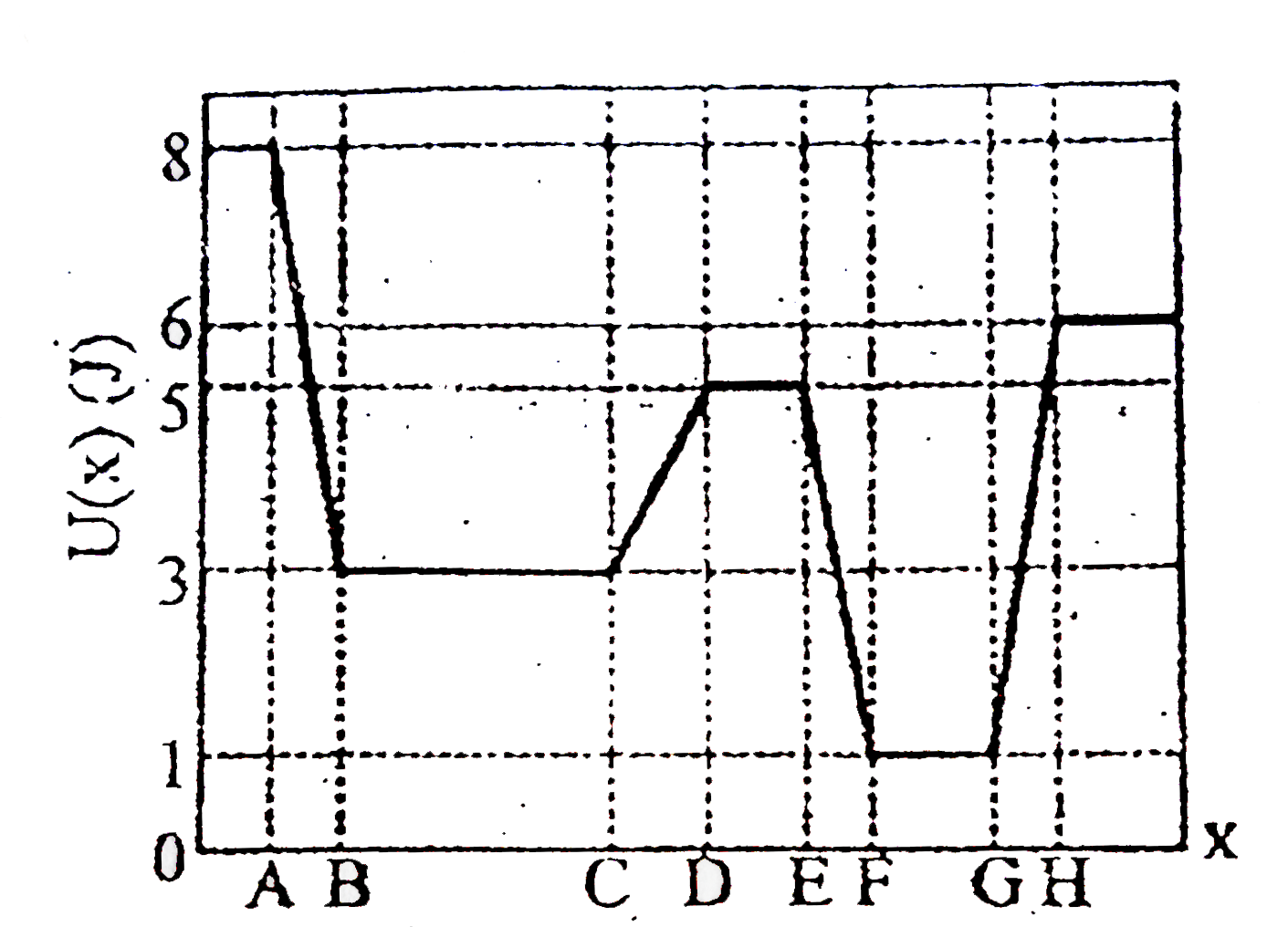 .
.
View SolutionIf x,F and U denote the dispalcement, force acting on and potential energy of a particle then
View SolutionA single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule where x is in meter. Then:
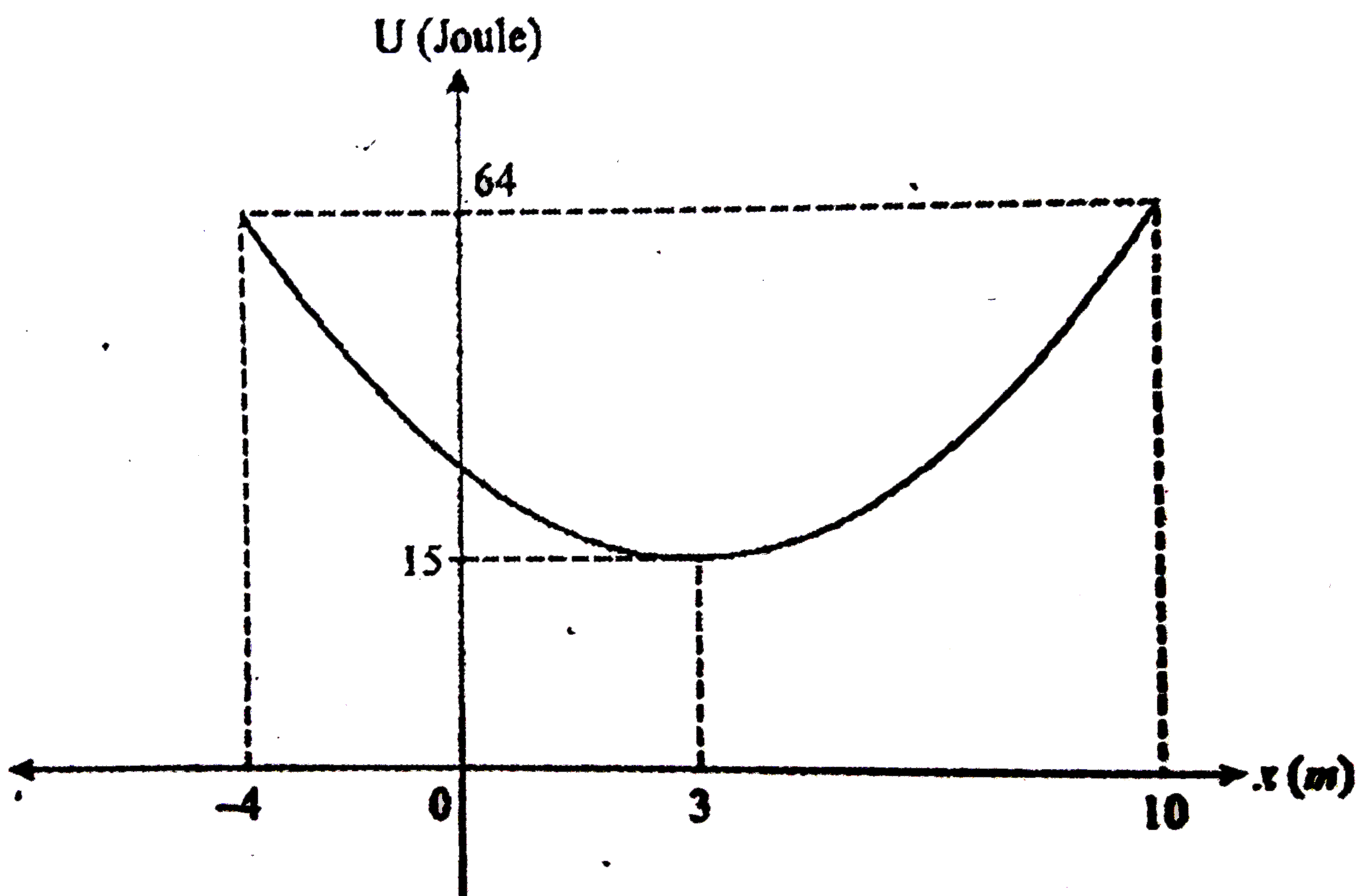
View Solution
