Two particles A and B start moving with velocities 20 m/s and 30√2 m/s along x-axis and at an angle 45∘ with x- axis respectively in xy-plane from origin the relative velocity of B w.r.t A
(10ˆi+30ˆj) m/s
(30ˆi+10ˆj) m/s
(30ˆi−20√2ˆj) m/s
(30√2ˆi+10√2ˆj) m/s
The correct Answer is:A
To find the relative velocity of particle B with respect to particle A, we can follow these steps:
Step 1: Identify the velocities of particles A and B.
- Particle A moves along the x-axis with a velocity of VA=20m/s.
- Particle B moves at an angle of 45∘ with the x-axis with a velocity of VB=30√2m/s.
Step 2: Break down the velocity of particle B into its components.
Since particle B is moving at an angle of 45∘, we can resolve its velocity into x and y components:
- The x-component of VB is given by:
VBx=VBcos(45∘)=30√2⋅1√2=30m/s
- The y-component of VB is given by:
VBy=VBsin(45∘)=30√2⋅1√2=30m/s
Thus, the velocity vector of particle B can be expressed as:
VB=30^i+30^jm/s
Step 3: Write the velocity vector of particle A.
Since particle A is moving along the x-axis, its velocity vector is:
VA=20^im/s
Step 4: Calculate the relative velocity of B with respect to A.
The relative velocity of B with respect to A, denoted as VBA, is calculated using the formula:
VBA=VB−VA
Substituting the values we found:
VBA=(30^i+30^j)−(20^i)=(30−20)^i+30^j=10^i+30^jm/s
Step 5: State the final answer.
The relative velocity of particle B with respect to particle A is:
VBA=10^i+30^jm/s
---
- Particle A moves along the x-axis with a velocity of VA=20m/s.
- Particle B moves at an angle of 45∘ with the x-axis with a velocity of VB=30√2m/s.
Since particle B is moving at an angle of 45∘, we can resolve its velocity into x and y components:
- The x-component of VB is given by:
VBx=VBcos(45∘)=30√2⋅1√2=30m/s
- The y-component of VB is given by:
VBy=VBsin(45∘)=30√2⋅1√2=30m/s
VB=30^i+30^jm/s
Since particle A is moving along the x-axis, its velocity vector is:
VA=20^im/s
The relative velocity of B with respect to A, denoted as VBA, is calculated using the formula:
VBA=VB−VA
VBA=(30^i+30^j)−(20^i)=(30−20)^i+30^j=10^i+30^jm/s
The relative velocity of particle B with respect to particle A is:
VBA=10^i+30^jm/s
Similar Questions
Two points "A" and "B" are moving with the same speed 'u=4*sqrt(2)m/s' in the positive direction of "x" -axis and "y" -axis respectively.Find the magnitude of relative velocity of "C" w.r.t. A (where "C" is the mid-point of "AB" )
View Solution[" Two points "A" and "B" are moving with the same "],[" speed "u=4sqrt(2)m/s" in the positive "],[" direction of "x" -axis and y-axis respectively.Find "],[" the magnitude of relative velocity of "C" w.r.t "],[" A (where "C" is the mid-point of "AB" )."]
View Solution
Knowledge Check
Particle A moves along X-axis with a uniform velocity of magnitude 10 m/s. Particle B moves with uniform velocity 20 m/s along a direction making an angle of 60° with the positive direction of X-axis as shown in the figure. The relative velocity of B with respect to that A is
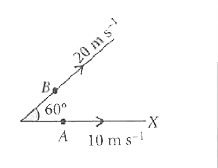 A10 m/s along X-axisB10√3 m/s along Y-axis (perpendicular to X-axis)C10√5 m/s along the bisection of the velocities of A and B.D30 m/s along negative X -axis.
A10 m/s along X-axisB10√3 m/s along Y-axis (perpendicular to X-axis)C10√5 m/s along the bisection of the velocities of A and B.D30 m/s along negative X -axis.Two particles P and Q start from origin and execute simple harmonic motion along X-axis with same amplitude but with periods 3s and 6s respectively. The ratio of the velocities of P and Q when they meet is
A1:2B2:1C2:3D3:2Two particles P and Q simultaneously start moving from point A with velocities 15m/s and 20m/s respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When P overtakes Q and B then its velocity is 30m/s the velocity of Q at point B will be
A30m/sB5m/sC10m/sD15m/s
A car A moves with velocity 15ms−1 and B with velocity 20ms−1 are moving in opposite directions as shown in . Find the relative velocity of B w.r.t. A and w.r.t. B.
 .
.
View SolutionA and B are moving with the same speed 10m/s in the direction E−30∘−N and E−30∘−S respectively. Find the relative velocity of A w.r.t. B.
View SolutionThe displacement-time graph of two particles A and B are straight line making angle of 60∘ and 45∘ with x-axis respectively. Then find the ratio of velocity of A and velocity of B.
View SolutionIf a particle A is moving along a straight line with velocity 3m/s and another particle B has a velocity 5m/s at an angle of 60∘ to the path of A then the velocity B relative to A is
View SolutionIf a particle A is moving along a straight line with velocity 3m/s and another particle B has a velocity 5m/s at an angle of 60∘ to the path of A then the velocity B relative to A is
View Solution
