Two stones are thrown with same speed u at different angles from ground n air if both stones have same range and height attained by them are h1andh2, then h1+h2 is equal to
u2g
u22g
u23g
u24g
The correct Answer is:B
To solve the problem, we need to find the sum of the heights attained by two stones thrown with the same speed u at different angles, given that they have the same range. Let's denote the heights attained by the stones as h1 and h2.
Step 1: Understand the Range and Height Formulas
The range R of a projectile is given by the formula:
R=u2sin2θg
where θ is the angle of projection, u is the initial speed, and g is the acceleration due to gravity.
The maximum height h attained by the projectile is given by:
h=u2sin2θ2g
Step 2: Set Up the Problem
Let the angles of projection for the two stones be θ1 and θ2. Since both stones have the same range, we can write:
u2sin2θ1g=u2sin2θ2g
This simplifies to:
sin2θ1=sin2θ2
Step 3: Analyze the Sine Function
The equation sin2θ1=sin2θ2 implies that:
2θ1=2θ2+nπor2θ1=π−2θ2+nπ
for some integer n. For angles in the range of projectile motion, we can conclude that:
θ1+θ2=90∘
This means θ2=90∘−θ1.
Step 4: Calculate Heights
Now we can calculate the heights h1 and h2:
- For h1:
h1=u2sin2θ12g
- For h2:
h2=u2sin2θ22g=u2sin2(90∘−θ1)2g=u2cos2θ12g
Step 5: Sum the Heights
Now we can find h1+h2:
h1+h2=u2sin2θ12g+u2cos2θ12g
Factoring out u22g:
h1+h2=u22g(sin2θ1+cos2θ1)
Using the Pythagorean identity sin2θ+cos2θ=1:
h1+h2=u22g⋅1=u22g
Final Answer
Thus, the sum of the heights attained by the two stones is:
h1+h2=u22g
The range R of a projectile is given by the formula:
R=u2sin2θg
where θ is the angle of projection, u is the initial speed, and g is the acceleration due to gravity.
h=u2sin2θ2g
Let the angles of projection for the two stones be θ1 and θ2. Since both stones have the same range, we can write:
u2sin2θ1g=u2sin2θ2g
This simplifies to:
sin2θ1=sin2θ2
The equation sin2θ1=sin2θ2 implies that:
2θ1=2θ2+nπor2θ1=π−2θ2+nπ
for some integer n. For angles in the range of projectile motion, we can conclude that:
θ1+θ2=90∘
This means θ2=90∘−θ1.
Now we can calculate the heights h1 and h2:
- For h1:
h1=u2sin2θ12g
- For h2:
h2=u2sin2θ22g=u2sin2(90∘−θ1)2g=u2cos2θ12g
Now we can find h1+h2:
h1+h2=u2sin2θ12g+u2cos2θ12g
Factoring out u22g:
h1+h2=u22g(sin2θ1+cos2θ1)
Using the Pythagorean identity sin2θ+cos2θ=1:
h1+h2=u22g⋅1=u22g
Thus, the sum of the heights attained by the two stones is:
h1+h2=u22g
Similar Questions
Two balls of different masses are thrown vertically upward with same initial velocity. Height attained by them are h1andh2 respectively. What is h1/h2 ?
View SolutionTwo balls of different masses are thrown vertically upward with same initial velocity. Height attained by them are h1andh2 respectively. What is h1/h2 ?
View Solution
Knowledge Check
- Question 1 - Select One
Two balls are thrown simultaneously at two different angles so that both have equal ranges. If H1 and H2 be the maximum heights attained in two cases. Then the summation H1+H2 is equal to
Av202gBv20gC2v20gDv204g - Question 2 - Select One
Two balls are thrown with the same speed from a point O at the same time so that their horizontal ranges are same. If the difference of the maximum height attained by them is equal to half of the sum of the maximum heights, then the angles of projection for the balls are
A15∘,75∘B30∘,60∘C0∘,90∘D37∘,53∘ - Question 3 - Select One
From the top of a tower, a stone is thrown up and reaches the ground in time t1=9s. a second stone is thrown down with the same speed and reaches the ground in time t2=4s. A third stone is released from rest and reaches the ground in time t3, which is equal to
A6.5 sB6.0 sC7213sDnone
When the angle of elevation of a gun are 60∘ and 30∘ respectively, the height it shoots are h1 and h2 respectively, h1/h2 equal to –
View SolutionThree projecties are thrown all with same speed u but at different angles of projection (θ>θ2>θ3) all taken from horizontal. Maximum height attained by projectile (3) is H. Range of (1) & (3) is same & that of (2) is maximum for the given speed. At height H, speeds are v1,v2&v3 as shown. Total time of flights are T1,T2&T3. Choose the correct statement(s).
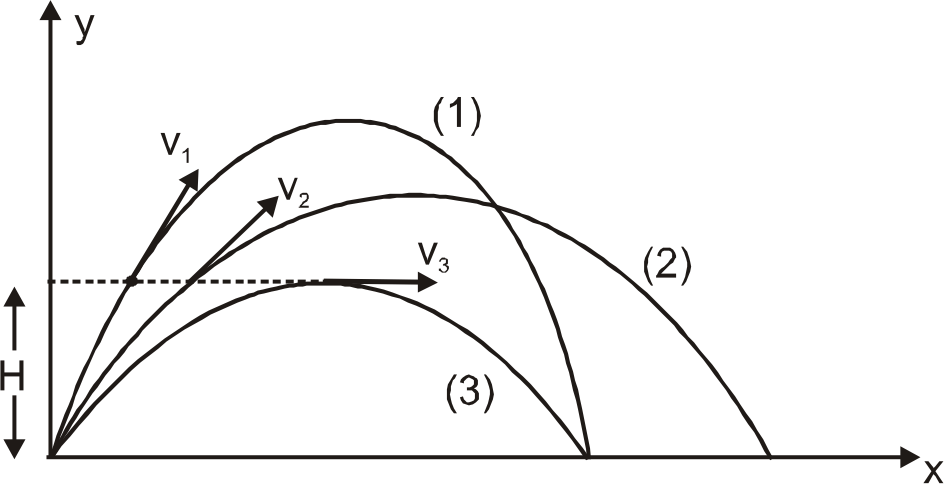 View Solution
View SolutionTwo stones are projected from level ground. Trajectory of two stones are shown in figure. Both stones have same maximum heights above level ground as shown. Let T1 and T2 be their time of flights and u1 and u2 be their speeds of projection respectively (neglect air resistance). then
 View Solution
View SolutionFrom the top of a tower, a stone is thrown up and it reaches the ground in time t1A second stone is thrown down with the same speed and it reaches the ground in time t2 A third stone is released from rest and it reaches the ground in time The correct relation between t1,t2 and t3 is :
View SolutionA stone thrown upward with a speed u from the top of a tower reaches the ground with a velocity 4u. The height of the tower is
View Solution

