A person aiming to reach exactly opposite point on the bank of a stream is swimming with a speed of 0.6 m/s at an angle of 120∘ with the direction of flow of water . The speed of water in the stream is
0.3 m/s
0.5 m/s
1.0 m/s
0.433 m/s
The correct Answer is:A
To solve the problem of a person swimming across a stream at an angle while trying to reach a point directly opposite on the bank, we can break down the situation step by step.
1. Understand the Problem:
The swimmer is swimming at a speed of 0.6m/s at an angle of 120∘ with respect to the direction of the flow of the water. We need to find the speed of the stream, denoted as U.
2. Identify the Components of Velocity:
The swimmer's velocity can be broken down into two components:
- Horizontal Component (along the direction of the stream): Vx=Vcos(120∘)
- Vertical Component (across the stream): Vy=Vsin(120∘)
Where V=0.6m/s.
3. Calculate the Components:
- The angle 120∘ can be converted to its reference angle 30∘ for calculations:
- Vx=0.6cos(120∘)=0.6cos(30∘+90∘)=−0.6cos(30∘)=−0.6×(−√32)=−0.3√3m/s
- Vy=0.6sin(120∘)=0.6sin(30∘)=0.6×12=0.3m/s
4. Condition for Reaching the Opposite Point:
For the swimmer to reach the point directly opposite, the horizontal component of the swimmer's velocity must be equal to the speed of the stream:
U=Vx
Therefore, we know:
U=0.6sin(30∘)
5. Calculate the Speed of the Stream:
Since sin(30∘)=12:
U=0.6×12=0.3m/s
Final Answer:
The speed of the stream is 0.3m/s.
The swimmer is swimming at a speed of 0.6m/s at an angle of 120∘ with respect to the direction of the flow of the water. We need to find the speed of the stream, denoted as U.
The swimmer's velocity can be broken down into two components:
- Horizontal Component (along the direction of the stream): Vx=Vcos(120∘)
- Vertical Component (across the stream): Vy=Vsin(120∘)
- The angle 120∘ can be converted to its reference angle 30∘ for calculations:
- Vx=0.6cos(120∘)=0.6cos(30∘+90∘)=−0.6cos(30∘)=−0.6×(−√32)=−0.3√3m/s
- Vy=0.6sin(120∘)=0.6sin(30∘)=0.6×12=0.3m/s
For the swimmer to reach the point directly opposite, the horizontal component of the swimmer's velocity must be equal to the speed of the stream:
U=Vx
Therefore, we know:
U=0.6sin(30∘)
Since sin(30∘)=12:
U=0.6×12=0.3m/s
The speed of the stream is 0.3m/s.
Similar Questions
A man can swim at a speed 2ms−1 in still water. He starts swimming in a river at an angle 150∘ with direction of flow of water and reaches at the exactly oppsite point on the opposite bank.
(a) Find the speed of flowing water.
(b) If width of river is 1 km then calculate the time taken also
View SolutionA swimmer wishes to reach directly opposite point on the other bank of a river,flowing with velocity 4√2ms.The swimmer can swim with 8ms in still water.The angle with the flow direction he should swim to reach the directly opposite point is (A)450 (B)900 (C)1350 (D)1500
View Solution
Knowledge Check
A person aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of 0.5ms at an angle of 120∘ with the direction of flow of water. The speed of water in the stream is
A1msB0.5msC0.25(m)/(s)D0.433msPerson aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of 0.5ms−1 at an angle of 120∘ with the direction of flow of water.The speed of water in the stream is
A1ms−1B0.25ms−1C0.67ms−1D3ms−1A person, reaches a point directly opposite on the other bank of a flowing river, while swimming at a speed of 5 m/s at an angle of 120∘ with the flow. The speed of the flow must be
A2.5 m/sB3 m/sC4 m/sD1.5 m/s
A person is swimming with a speed of 10 m/s at an angle of 120° with the flow and reaches to a point directly opposite on the other side of the river. The speed of the flow is 'x m/s.
The value of 'x to the nearest integer is_________.
View SolutionA man can row with a speed of 6 km/h in still water. What will be his speed with the stream, if the speed of stream is 2 km/h?
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the fig 1E.125 (a) what minimum speed relative to water should the man have so that he can reach point B directly by swimming? In which direction should he swin?
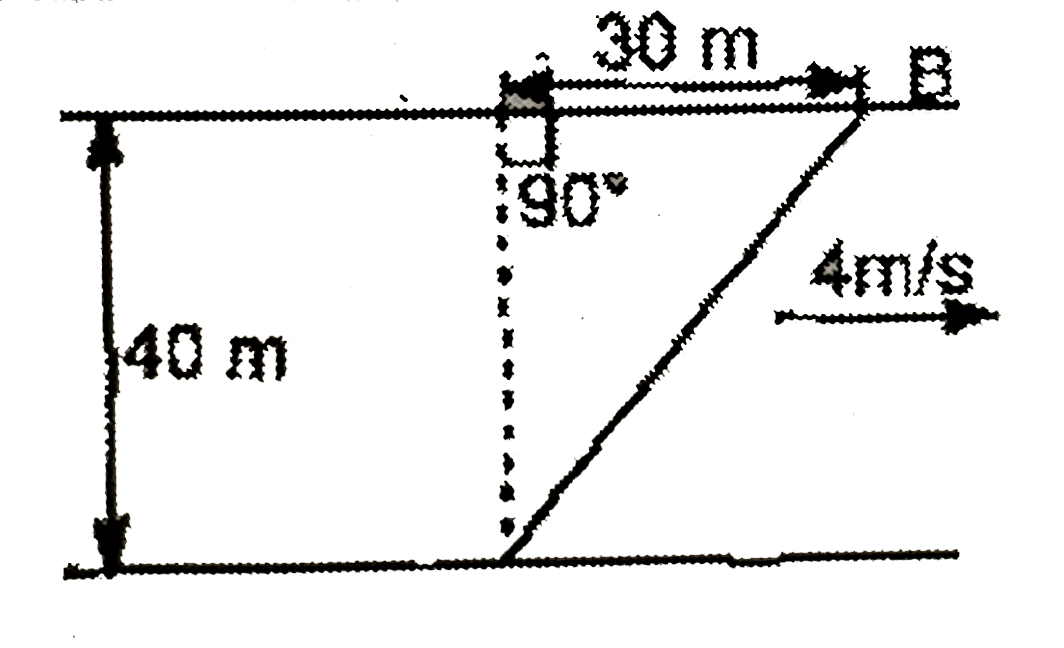
View SolutionA man can swim in still water at a speed of 6kmph and he has to cross the river and reach just opposite point on the other bank.If the river is flowing at a speed of 3kmph,and the width of the river is 2km, the time taken to cross the river is (in hours)
View SolutionA man who can swin at the rate of 2 kmhr)(in still river) crosses a river to a point exactly opposite on the other bank by swimming in a direction of 120∘ to the flow of the water in the river. The velocity of the water current in kmhr is
View Solution
